
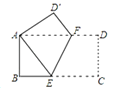
【题目】如图,在矩形ABCD中,AB=4,BC=8,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为_____.
【答案】![]()
【解析】
设BE=x,表示出CE=8x,根据翻折的性质可得AE=CE,然后在Rt△ABE中,利用勾股定理列出方程求出x,再根据翻折的性质可得∠AEF=∠CEF,根据两直线平行,内错角相等可得∠AFE=∠CEF,然后求出∠AEF=∠AFE,根据等角对等边可得AE=AF,过点E作EH⊥AD于H,可得四边形ABEH是矩形,根据矩形的性质求出EH、AH,然后求出FH,再利用勾股定理列式计算即可得解.
解:设BE=x,则CE=BCBE=8x,
∵沿EF翻折后点C与点A重合,
∴AE=CE=8x,
在Rt△ABE中,AB2+BE2=AE2,即42+x2=(8x)2,
解得:x=3,
∴AE=83=5,
由翻折的性质得,∠AEF=∠CEF,
∵AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF=5,
过点E作EH⊥AD于H,则四边形ABEH是矩形,
∴EH=AB=4,AH=BE=3,
∴FH=AFAH=53=2,
在Rt△EFH中,EF=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】现在越来越多的人在用微信付款、转账,也可以提现.把微信账户里的钱转到银行卡里叫做提现.从2016年3月1日起,每个微信账户终身享有![]() 元免费提现额度,当累计提现额度超过
元免费提现额度,当累计提现额度超过![]() 元时,超出
元时,超出![]() 元的部分要支付
元的部分要支付![]() 的手续费.以后每次提现都要支付所提现金额的
的手续费.以后每次提现都要支付所提现金额的![]() 的手续费.
的手续费.
(1)张老师在今年第一次进行了提现,金额为![]() 元,他需要支付手续费 元.
元,他需要支付手续费 元.
(2)李老师从2016年3月1日起至今,用自己的微信账户共提现![]() 次,
次, ![]() 次提现的金额和手续费如下表:
次提现的金额和手续费如下表:
第一次提现 | 第二次提现 | 第三次提现 | |
提现金额(元) |
|
|
|
手续费(元) |
|
|
|
请问李老师前![]() 次提现的金额分别是多少元?
次提现的金额分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
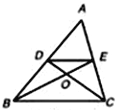
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=﹣2x+1,下列结论正确的是( )
A. 图象必经过点(﹣2,1) B. 图象经过第一、二、三象限
C. 当x>![]() 时,y<0 D. y随x的增大而增大
时,y<0 D. y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 在平面直角坐标系中与
在平面直角坐标系中与![]() 轴交于点A,点B(-3,3)也在直线
轴交于点A,点B(-3,3)也在直线![]() 上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线
上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线![]() 上.
上.
(1)求点C的坐标和直线![]() 的解析式;
的解析式;
(2)已知直线![]() :
:![]() 经过点B,与
经过点B,与![]() 轴交于点E,求△ABE的面积.
轴交于点E,求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=-![]() 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.


(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
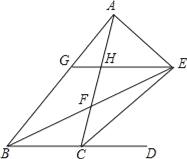
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人同时开车从A地出发,沿一条笔直的公路匀速前往相距400千米的B地,1小时后,甲发现有物品落在A地,于是立即按原速返回A地取物品,取到物品后立即提速25%继续开往B地(所有掉头和取物品的时间忽略不计),甲乙两人间的距离y千米与甲开车行驶的时间x小时之间的部分函数图象如图所示,当甲到达B地时,乙离B地的距离是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com