
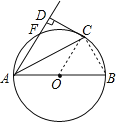
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】 (2)4
【解析】
试题(1)连结OC,由![]() =
=![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由![]() =
=![]() =
=![]() ,得∠BOC=60°,则∠BAC=30°,所以
,得∠BOC=60°,则∠BAC=30°,所以
∠DAC=30°,在Rt△ADC中,利用含30°的直角三角形三边的关系得AC=2CD=4![]() ,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=
,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=![]() AC=4,AB=2BC=8,所以⊙O的半径为4.
AC=4,AB=2BC=8,所以⊙O的半径为4.
试题解析:(1)证明:连结OC,如图,
∵![]() =
=![]()
∴∠FAC=∠BAC
∵OA=OC
∴∠OAC=∠OCA
∴∠FAC=∠OCA
∴OC∥AF
∵CD⊥AF
∴OC⊥CD
∴CD是⊙O的切线
(2)解:连结BC,如图
∵AB为直径
∴∠ACB=90°
∵![]() =
=![]() =
=![]()
∴∠BOC=![]() ×180°=60°
×180°=60°
∴∠BAC=30°
∴∠DAC=30°
在Rt△ADC中,CD=2![]()
∴AC=2CD=4![]()
在Rt△ACB中,BC=![]() AC=
AC=![]() ×4
×4![]() =4
=4
∴AB=2BC=8
∴⊙O的半径为4.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
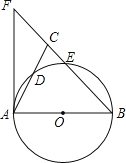
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
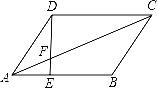
【题目】已知如图,平行四边形ABCD中,AE:EB=1:2.
(1)求AE:DC的值.
(2)△AEF与△CDF相似吗?若相似,请说明理由,并求出相似比.
(3)如果S△AEF=6cm2,求S△CDF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
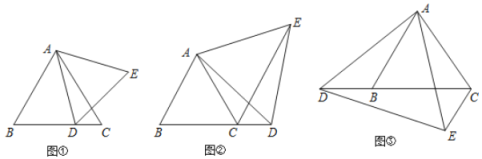
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com