
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
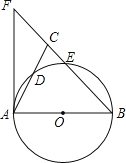
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
【答案】(1)见解析;(2)CE=2.
【解析】
(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2求得答案.
)2=x2+(3x)2求得答案.
(1)证明:如图,连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
即∠DAB+∠CAF=90°.
∴∠CAF=∠ABD.
∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.
∴∠ABC=2∠CAF.
(2)解:如图,连接AE,
∴∠AEB=90°,
设CE=x,
∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,
在Rt△ACE中,AC2=CE2+AE2,
即(2![]() )2=x2+(3x)2,
)2=x2+(3x)2,
∴x=2.
∴CE=2.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,6),点B(4,3),P是x轴上的一个动点.作OQ⊥AP,垂足为点Q,连接QB,则△AQB的面积的最大值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:
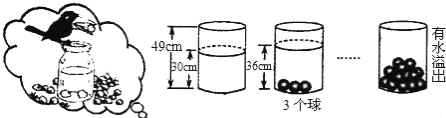
(1)放入一个小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的函数关系式;
(3)当量桶中水面上升至距离量桶顶部3cm时,应在量桶中放入几个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在越来越多的人在用微信付款、转账,也可以提现.把微信账户里的钱转到银行卡里叫做提现.从2016年3月1日起,每个微信账户终身享有![]() 元免费提现额度,当累计提现额度超过
元免费提现额度,当累计提现额度超过![]() 元时,超出
元时,超出![]() 元的部分要支付
元的部分要支付![]() 的手续费.以后每次提现都要支付所提现金额的
的手续费.以后每次提现都要支付所提现金额的![]() 的手续费.
的手续费.
(1)张老师在今年第一次进行了提现,金额为![]() 元,他需要支付手续费 元.
元,他需要支付手续费 元.
(2)李老师从2016年3月1日起至今,用自己的微信账户共提现![]() 次,
次, ![]() 次提现的金额和手续费如下表:
次提现的金额和手续费如下表:
第一次提现 | 第二次提现 | 第三次提现 | |
提现金额(元) |
|
|
|
手续费(元) |
|
|
|
请问李老师前![]() 次提现的金额分别是多少元?
次提现的金额分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,将矩形沿AE折叠,点B落在点B'处,当△B'EC是直角三角形时,BE的长为( )
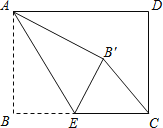
A.2B.6C.3或6D.2或3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接购物节,某网店准备购进甲、乙两种运动鞋,甲种运动鞋每双的进价比乙种运动鞋每双的进价多60元,用30000元购进甲种运动鞋的数量与用21000元购进乙种运动鞋的数量相同.
(1)求甲、乙两种运动鞋的进价(用列分式方程的方法解答):
(2)该网店老板计划购进这两种运动鞋共200双,且甲种运动鞋的进货数量不少于乙种运动鞋数量的![]() ,甲种运动鞋每双售价为350元,乙种运动鞋每双售价为300元.设甲种运动鞋的进货量为m双,销售完甲、乙两种运动鞋的总利润为w元,求w与m的函数关系式,并求总利润的最大值.
,甲种运动鞋每双售价为350元,乙种运动鞋每双售价为300元.设甲种运动鞋的进货量为m双,销售完甲、乙两种运动鞋的总利润为w元,求w与m的函数关系式,并求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,有一等腰直角三角形OAB,∠OAB=90°,直角边OA在x轴正半轴上,且OA=1,将Rt△OAB绕原点顺时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OA1B1(即A1O=2AO).同理,将Rt△OA1B1顺时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OA2B2……依此规律,得到等腰直角三角形OA2014B2014,则A2014点的坐标为( )
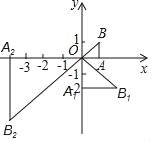
A. (0,22014) B. (0,﹣22014) C. (22014,0) D. (﹣22014,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com