
ΓΨΧβΡΩΓΩΗυΨί“‘œ¬10Ηω≥ΥΜΐΘ§ΜΊ¥πΈ ΧβΘΚ
ΓΓ11ΓΝ29ΘΜ12ΓΝ28ΘΜ13ΓΝ27ΘΜ14ΓΝ26ΘΜ15ΓΝ25ΘΜ16ΓΝ24ΘΜ17ΓΝ23ΘΜ18ΓΝ22ΘΜ19ΓΝ21ΘΜ20ΓΝ20Θ°
Θ®1Θ©ΫΪ“‘…œΗς≥ΥΜΐΖ÷±π–¥≥…ΓΑa2©¹b2Γ±(ΝΫ ΐΤΫΖΫ)ΒΡ–Έ ΫΘ§ΫΪ“‘…œ10Ηω≥ΥΜΐΑ¥’’¥”–ΓΒΫ¥σΒΡΥ≥–ρ≈≈Ν–Τπά¥ΘΜ
Θ®2Θ©”ΟΚ§”–aΘ§bΒΡ ΫΉ”±μ ΨΘ®1Θ©÷–ΒΡ“ΜΗω“ΜΑψ–‘ΒΡΫα¬έ(≤Μ“Σ«σ÷ΛΟς)ΘΜ
Θ®3Θ©ΗυΨίΘ®2Θ©÷–ΒΡ“ΜΑψ–‘ΒΡΫα¬έΜΊ¥πœ¬ΟφΈ ΧβΘΚΡ≥÷÷≤ζΤΖΒΡ‘≠ΝœΧαΦέΘ§“ρΕχ≥ßΦ“ΨωΕ®Ε‘≤ζΤΖΫχ––ΧαΦέΘ§œ÷”–ΝΫ÷÷ΖΫΑΗΖΫΑΗΘΚΒΎ“Μ¥ΈΧαΦέp%Θ§ΒΎΕΰ¥ΈΧαΦέq%ΘΜΖΫΑΗ2ΘΚΒΎ“ΜΓΔΕΰ¥ΈΧαΦέΨυΈΣ![]() %Θ§Τδ÷–pΓΌqΘ§±»ΫœΡΡ÷÷ΖΫΑΗΧαΦέΉνΕύΘΩ
%Θ§Τδ÷–pΓΌqΘ§±»ΫœΡΡ÷÷ΖΫΑΗΧαΦέΉνΕύΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©¥πΑΗΦϊΫβΈωΘΜΘ®2Θ©Ε‘”ΎΘΚabΘ§Β±|b©¹a|‘Ϋ¥σ ±Θ§abΒΡ÷Β‘Ϋ–ΓΘΜΘ®3Θ©ΖΫΑΗ2ΧαΦέΉνΕύΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΧβΡΩ÷–ΒΡ ΫΉ”ΚΆΤΫΖΫ≤νΙΪ ΫΩ…“‘Ϋβ¥π±ΨΧβΘΜ
Θ®2Θ©ΗυΨίΘ®1Θ©÷–ΒΡΦΤΥψΫαΙϊΘ§Ω…“‘–¥≥ωœύ”ΠΒΡΫα¬έΘΜ
Θ®3Θ©ΗυΨίΧβ“βΝ–≥ω¥ζ ΐ ΫΘ§ΗυΨίΘ®2Θ©÷–ΒΡΫα¬έΩ…“‘Ϋβ¥π±ΨΧβΘ°
Θ®1Θ©11ΓΝ29=(20©¹9)ΓΝ(20+9)=202©¹92Θ§
12ΓΝ28=(20©¹8)ΓΝ(20+8)=202©¹82Θ§
13ΓΝ27=(20©¹7)ΓΝ(20+7)=202©¹72Θ§
14ΓΝ26=(20©¹6)ΓΝ(20+6)=202©¹62
15ΓΝ25=(20©¹5)ΓΝ(20+5)=202©¹52Θ§
16ΓΝ24=(20©¹4)ΓΝ(20+4)=202©¹42
17ΓΝ23=(20©¹3)ΓΝ(20+3)=202©¹32Θ§
18ΓΝ22=(20©¹2)ΓΝ(20+2)=202©¹22Θ§
19ΓΝ21=(20©¹1)ΓΝ(20+1)=202©¹12Θ§
20ΓΝ20=(20+0)ΓΝ(20©¹0)=202©¹02Θ§
11ΓΝ29ΘΦ12ΓΝ28ΘΦ13ΓΝ27ΘΦ14ΓΝ26ΘΦ15ΓΝ25ΘΦ16ΓΝ24ΘΦ17ΓΝ23ΘΦ18ΓΝ22ΘΦ19ΓΝ21ΘΦ20ΓΝ20ΘΜ
Θ®2Θ©”…Θ®1Θ©Ω…ΒΟΘΚΕ‘”ΎabΘ§Β±|b©¹a|‘Ϋ¥σ ±Θ§abΒΡ÷Β‘Ϋ–ΓΘΜ
Θ®3Θ©…η‘≠ΦέΈΣaΘ§‘ρ
ΖΫΑΗ1ΘΚa(1+p%)(1+q%)
ΖΫΑΗ2ΘΚa(1![]() )2
)2
ΓΏ|1+p%©¹(1+q%)|=|(p©¹q)%|Θ§
|1![]() (1
(1![]() )|=0Θ°
)|=0Θ°
ÿpüqȧ
Γύ|(p©¹q)%|ΘΨ0Θ§
Γύ”…Θ®2Θ©ΒΡΫα¬έΩ…÷ΣΘΚ
ΖΫΑΗ2ΧαΦέΉνΕύΘ°


 ΡήΝΠΤάΦέœΒΝ–¥πΑΗ
ΡήΝΠΤάΦέœΒΝ–¥πΑΗ ΧΤ”ΓΈΡΜ·ΩΈ ±≤βΤάœΒΝ–¥πΑΗ
ΧΤ”ΓΈΡΜ·ΩΈ ±≤βΤάœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙΊ”ΎΚ· ΐy=©¹2x+1Θ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
A. ΆΦœσ±ΊΨ≠ΙΐΒψΘ®©¹2Θ§1Θ© B. ΆΦœσΨ≠ΙΐΒΎ“ΜΓΔΕΰΓΔ»ΐœσœό
C. Β±xΘΨ![]() ±Θ§yΘΦ0 D. yΥφxΒΡ‘ω¥σΕχ‘ω¥σ
±Θ§yΘΦ0 D. yΥφxΒΡ‘ω¥σΕχ‘ω¥σ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
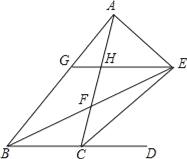
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΒΡΡΎΫ«ΓœABCΚΆΆβΫ«ΓœACDΒΡΤΫΖ÷œΏœύΫΜ”ΎΒψEΘ§BEΫΜAC”ΎΒψFΘ§ΙΐΒψEΉςEGΓΈBDΫΜAB”ΎΒψGΘ§ΫΜAC”ΎΒψHΘ§Ν§Ϋ”AEΘ§”–“‘œ¬Ϋα¬έΘΚ
ΔΌΓœBEC=![]() ΓœBACΘΜΔΎΓςHEFΓ’ΓςCBFΘΜΔέBG=CH+GHΘΜΔήΓœAEB+ΓœACE=90ΓψΘ§Τδ÷–’ΐ»ΖΒΡΫα¬έ”–_____Θ®ΫΪΥυ”–’ΐ»Ζ¥πΑΗΒΡ–ρΚ≈Χν–¥‘ΎΚαœΏ…œΘ©Θ°
ΓœBACΘΜΔΎΓςHEFΓ’ΓςCBFΘΜΔέBG=CH+GHΘΜΔήΓœAEB+ΓœACE=90ΓψΘ§Τδ÷–’ΐ»ΖΒΡΫα¬έ”–_____Θ®ΫΪΥυ”–’ΐ»Ζ¥πΑΗΒΡ–ρΚ≈Χν–¥‘ΎΚαœΏ…œΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
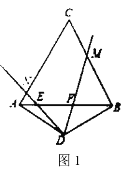
ΓΨΧβΡΩΓΩΥΡ±Ώ–Έ![]() «”…Β»±Ώ
«”…Β»±Ώ![]() ΚΆΕΞΫ«ΈΣ120ΓψΒΡΒ»―ϋ»ΐΫ«–Έ
ΚΆΕΞΫ«ΈΣ120ΓψΒΡΒ»―ϋ»ΐΫ«–Έ![]() Τ¥≥…Θ§ΫΪ“ΜΗω60ΓψΫ«ΕΞΒψΖ≈‘ΎΒψ
Τ¥≥…Θ§ΫΪ“ΜΗω60ΓψΫ«ΕΞΒψΖ≈‘ΎΒψ![]() ¥ΠΘ§60ΓψΫ«ΝΫ±ΏΖ÷±πΫΜ÷±œΏ
¥ΠΘ§60ΓψΫ«ΝΫ±ΏΖ÷±πΫΜ÷±œΏ![]() ”Ύ
”Ύ![]() Θ§ΫΜ÷±œΏ
Θ§ΫΜ÷±œΏ![]() ”Ύ
”Ύ![]() ΝΫΒψΘ°
ΝΫΒψΘ°
Θ®1Θ©Β±![]() ΕΦ‘ΎœΏΕΈ
ΕΦ‘ΎœΏΕΈ![]() …œ ±Θ§ΧΫΨΩ
…œ ±Θ§ΧΫΨΩ![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘΜ
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘΜ
Θ®2Θ©Β±![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§«σ÷ΛΘΚ
ΒΡ―”≥ΛœΏ…œ ±Θ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”Ύ Β ΐaΘ§bΘ§Έ“Ο«Ω…“‘”Οmin{aΘ§b}±μ ΨaΘ§bΝΫ ΐ÷–Ϋœ–ΓΒΡ ΐΘ§άΐ»γmin{3Θ§Θ≠1}ΘΫΘ≠1Θ§min{2Θ§2}ΘΫ2. άύΥΤΒΊΘ§»τΚ· ΐy1ΓΔy2ΕΦ «xΒΡΚ· ΐΘ§‘ρyΘΫmin{y1Θ§ y2}±μ ΨΚ· ΐy1ΚΆy2ΒΡΓΑ»Γ–ΓΚ· ΐΓ±Θ°
Θ®1Θ©…ηy1ΘΫxΘ§y2ΘΫ![]() Θ§‘ρΚ· ΐyΘΫmin{xΘ§
Θ§‘ρΚ· ΐyΘΫmin{xΘ§ ![]() }ΒΡΆΦœώ”ΠΗΟ « ÷–ΒΡ ΒœΏ≤ΩΖ÷Θ°
}ΒΡΆΦœώ”ΠΗΟ « ÷–ΒΡ ΒœΏ≤ΩΖ÷Θ°

Θ®2Θ©«κ‘Ύœ¬ΆΦ÷–”Ο¥÷ ΒœΏΟη≥ωΚ· ΐyΘΫmin{(xΘ≠2)2Θ§ (xΘΪ2)2}ΒΡΆΦœώΘ§≤Δ–¥≥ωΗΟΆΦœώΒΡ»ΐΧθ≤ΜΆ§–‘÷ ΘΚ

ΔΌ ΘΜ
ΔΎ ΘΜ
Δέ ΘΜ
Θ®3Θ©Κ· ΐyΘΫmin{(xΘ≠4)2Θ§ (xΘΪ2)2}ΒΡΆΦœώΙΊ”Ύ Ε‘≥ΤΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡœ…≥»ΚΒΚ «Έ“ΙζΙΧ”–ΝλΆΝΘ§œ÷‘ΎΈ“ΡœΚΘ”φΟώ“Σ‘ΎΡœ…≥Ρ≥ΚΘΒΚΗΫΫϋΫχ––≤Ε”ψΉς“ΒΘ§Β±”φ¥§ΚΫ––÷ΝB¥Π ±Θ§≤βΒΟΗΟΒΚΈΜ”Ύ’ΐ±±ΖΫœρ![]() ΚΘάοΒΡC¥ΠΘ§ΈΣΝΥΖά÷ΙΡ≥ΙζΜΙ―≤Ψ·Η…»≈Θ§ΨΆ«κ«σΈ“A¥ΠΒΡ”ψΦύ¥§«ΑΆυC¥ΠΜΛΚΫΘ§“―÷ΣCΈΜ”ΎA¥ΠΒΡ±±ΤΪΕΪ45ΓψΖΫœρ…œΘ§AΈΜ”ΎBΒΡ±±ΤΪΈς30ΓψΒΡΖΫœρ…œΘ§«σAΓΔC÷°ΦδΒΡΨύάκΘ°
ΚΘάοΒΡC¥ΠΘ§ΈΣΝΥΖά÷ΙΡ≥ΙζΜΙ―≤Ψ·Η…»≈Θ§ΨΆ«κ«σΈ“A¥ΠΒΡ”ψΦύ¥§«ΑΆυC¥ΠΜΛΚΫΘ§“―÷ΣCΈΜ”ΎA¥ΠΒΡ±±ΤΪΕΪ45ΓψΖΫœρ…œΘ§AΈΜ”ΎBΒΡ±±ΤΪΈς30ΓψΒΡΖΫœρ…œΘ§«σAΓΔC÷°ΦδΒΡΨύάκΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉ““ΝΫ»ΥΆ§ ±ΩΣ≥Β¥”AΒΊ≥ωΖΔΘ§―Ί“ΜΧθ± ÷±ΒΡΙΪ¬Ζ‘»ΥΌ«ΑΆυœύΨύ400«ßΟΉΒΡBΒΊΘ§1–Γ ±ΚσΘ§ΦΉΖΔœ÷”–ΈοΤΖ¬δ‘ΎAΒΊΘ§”Ύ «ΝΔΦ¥Α¥‘≠ΥΌΖΒΜΊAΒΊ»ΓΈοΤΖΘ§»ΓΒΫΈοΤΖΚσΝΔΦ¥ΧαΥΌ25%ΦΧ–χΩΣΆυBΒΊΘ®Υυ”–ΒτΆΖΚΆ»ΓΈοΤΖΒΡ ±ΦδΚω¬‘≤ΜΦΤΘ©Θ§ΦΉ““ΝΫ»ΥΦδΒΡΨύάκy«ßΟΉ”κΦΉΩΣ≥Β–– ΜΒΡ ±Φδx–Γ ±÷°ΦδΒΡ≤ΩΖ÷Κ· ΐΆΦœσ»γΆΦΥυ ΨΘ§Β±ΦΉΒΫ¥οBΒΊ ±Θ§““άκBΒΊΒΡΨύάκ «_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
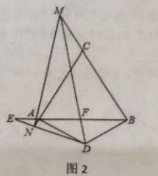
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§BAΘΫBCΘ§CDΚΆBE «ΓςABCΒΡΝΫΧθΗΏΘ§ΓœBCDΘΫ45ΓψΘ§BE”κCDΫΜ”ΎΒψHΘ°

Θ®1Θ©«σ÷ΛΘΚΓςBDHΓ’ΓςCDAΘΜ
Θ®2Θ©«σ÷ΛΘΚBHΘΫ2AEΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗΏ÷–’–…ζ÷Η±ξΒΫ–Θ «Έ“ –÷–ΩΦ’–…ζ÷ΤΕ»ΗΡΗοΒΡ“Μœν÷Ί“Σ¥κ ©Θ°Ρ≥≥θΦΕ÷–―ßΕ‘ΗΟ–ΘΫϋΥΡΡξ÷Η±ξΒΫ–Θ±ΘΥΆ…ζ»Υ ΐΫχ––ΝΥΆ≥ΦΤΘ§÷Τ≥…ΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
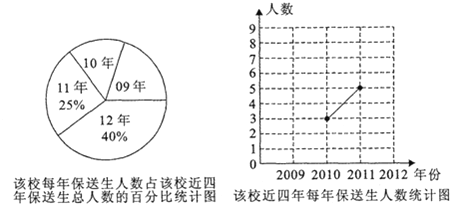
Θ®1Θ©ΗΟ–ΘΫϋΥΡΡξ±ΘΥΆ…ζ»Υ ΐΒΡΦΪ≤ν « Θ°«κΫΪ’έœΏΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©ΗΟ–Θ2009Ρξ÷Η±ξΒΫ–Θ±ΘΥΆ…ζ÷–÷Μ”–1ΈΜ≈°Ά§―ßΘ§―ß–Θ¥ρΥψ¥”÷–ΥφΜζ―Γ≥ω2ΈΜΆ§―ßΝΥΫβΥϊΟ«Ϋχ»ΥΗΏ÷–ΫΉΕΈΒΡ―ßœΑ«ιΩωΘ°«κ”ΟΝ–±μΖ®ΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®Θ§«σ≥ωΥυ―ΓΝΫΈΜΆ§―ß«ΓΚΟ «1ΈΜΡ–Ά§―ßΚΆ1ΈΜ≈°Ά§―ßΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com