
����Ŀ����������ָ�굽У�������п������ƶȸĸ��һ����Ҫ��ʩ��ij������ѧ�Ը�У������ָ�굽У����������������ͳ�ƣ��Ƴ�������������������ͳ��ͼ��
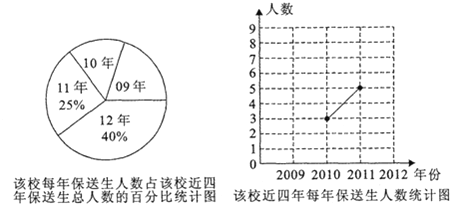
��1����У�����걣���������ļ����� ���뽫����ͳ��ͼ����������
��2����У2009��ָ�굽У��������ֻ��1λŮͬѧ��ѧУ����������ѡ��2λͬѧ�˽����ǽ��˸��нε�ѧϰ����������б�������״ͼ�ķ����������ѡ��λͬѧǡ����1λ��ͬѧ��1λŮͬѧ�ĸ��ʣ�
���𰸡��⣺��1����Ϊ��У�����걣�������������ֵ��8����Сֵ��3��
���Ը�У�����걣���������ļ����ǣ�8��3=5��
����ͳ��ͼ���£�
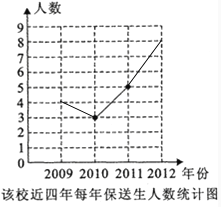
��2���б����£�
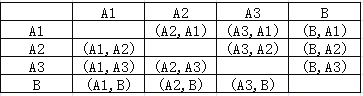
��ͼ����֪������12�������ѡ��λͬѧǡ����1λ��ͬѧ��1λŮͬѧ����6�������
����ѡ��λͬѧǡ����1λ��ͬѧ��1λŮͬѧ�ĸ�����![]() =
=![]() ��
��
����������1���ø�У�����걣�������������ֵ��ȥ��Сֵ��������������������ͳ��ͼ������ͳ��ͼ�ֱ����2009���2012��ı��������������ɽ�����ͳ��ͼ����������
��2�����������б��������������������ѡ��λͬѧǡ����1λ��ͬѧ��1λŮͬѧ��������ٸ��ݸ��ʹ�ʽ���㼴�ɣ�


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������10���˻����ش����⣺
��11��29��12��28��13��27��14��26��15��25��16��24��17��23��18��22��19��21��20��20��
��1�������ϸ��˻��ֱ�д�ɡ�a2��b2��(����ƽ��)����ʽ��������10���˻����մ�С�����˳������������
��2���ú���a��b��ʽ�ӱ�ʾ��1���е�һ��һ���ԵĽ���(��Ҫ��֤��)��
��3�����ݣ�2���е�һ���ԵĽ��ۻش��������⣺ij�ֲ�Ʒ��ԭ����ۣ�������Ҿ����Բ�Ʒ������ۣ��������ַ�����������һ�����p%���ڶ������q%������2����һ��������۾�Ϊ![]() %������p��q���Ƚ����ַ��������ࣿ
%������p��q���Ƚ����ַ��������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·����һ��ɽ������Ҫ��һ��������Ϊ�˼ӿ�ʩ�����ȣ�����Сɽ����һ��ͬʱʩ����Ϊ��ʹɽ����һ��Ŀ��ڵ�C��AB���ӳ����ϣ������C����ֱ��AB�Ĵ���L������B��һֱ�ߣ���ɽ���Ա߾���������L�ཻ��D�㣬��������ABD=135�㣬BD=800�ף���ֱ��L�Ͼ���D���Զ��C�����ڣ���![]() ��1.414����ȷ��1�ף�
��1.414����ȷ��1�ף�
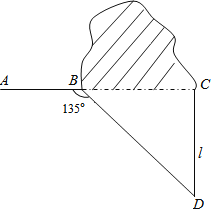
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6cm����ABC=30��������P�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��6��������PQ����PQΪֱ������O��
cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��6��������PQ����PQΪֱ������O��
��1����t=1ʱ������BPQ�������
��2�����O�����Ϊy����y��t�ĺ�������ʽ��
��3������O��Rt��ABC��һ�������У���t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
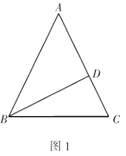
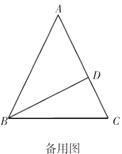
��ͼ1��![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
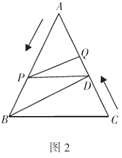
��![]() ����ͼ2����ͼ1�Ļ����ϣ�����
����ͼ2����ͼ1�Ļ����ϣ�����![]() �ӵ�
�ӵ�![]() ������ÿ��
������ÿ��![]() ���ٶ����߶�
���ٶ����߶�![]() ���
���![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������ͬ�ٶ����߶�
��������ͬ�ٶ����߶�![]() ���
���![]() �˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������
�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() �룮
�룮
��1����![]() �ij���
�ij���
��2����![]() ������һ����
������һ����![]() ƽ��ʱ��
ƽ��ʱ��![]() ��
��![]() ���غϣ�����
���غϣ�����![]() ��ֵ��
��ֵ��
��3����![]() ���߶�
���߶�![]() ���˶��Ĺ����У��Ƿ������
���˶��Ĺ����У��Ƿ������![]() Ϊ����
Ϊ����![]() �ǵ��������Σ������ڣ����
�ǵ��������Σ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
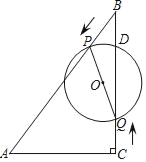
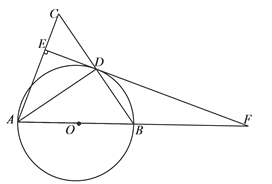
����Ŀ����ͼ���ڡ�ABC����AB=AC����ABΪֱ������ԲO����BC�ڵ�D������AD������D��DE��AC������Ϊ��E����AB���ӳ����ڵ�F��
��1����֤��EF�ǡ�O��������
��2�������O�İ뾶Ϊ5��sin��ADE=![]() ����BF�ij���
����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڡ������������С��ж��У�ij�����ƻ������Ϊ2160m2����������̻�����Ͷ�꣬�ɼס����������̶�����ɣ���֪��ÿ��������̻���������Ҷ�ÿ��������̻������2���������ڶ���������Ϊ480m2������̻�ʱ���ӱ��Ҷ�����4�죮
��1����ס��������̶�ÿ��������̻��������
��2������̶�ʩ��x�죬�ҹ��̶�ʩ��y�죬�պ�����̻�������y��x�ĺ�������ʽ��
��3������ÿ���̻�������0.8��Ԫ���Ҷ�ÿ���̻�����Ϊ0.35��Ԫ���Ҽס�������ʩ����������������26�죬����ΰ��ż�������ʩ����������ʹʩ���ܷ�����ͣ��������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ����Ϊ2m����Ϊ2m�ij�����ֽƬ���ü�����ͼ���������Ŀ���״��С��ȫһ����С������ֽƬ��Ȼ��ͼ2�ķ�ʽƴ��1�����������Σ�����Ӱ����Ϊ���ģ�
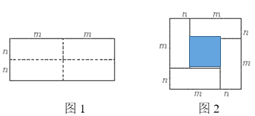
��1�����������ַ�����ͼ2����Ӱ���ֵ������ֱ���ú�m��n�Ĵ���ʽ��ʾ�������� �������� ��
��2���۲�ͼ2������д��![]()
![]() ��
��![]() ��������ʽ֮����ڵĺ�ȹ�ϵʽ��
��������ʽ֮����ڵĺ�ȹ�ϵʽ��
��3����֪![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ��ĶԳ���Ϊֱ��x=1���ң�x1��y1������x2��y2��Ϊ��ͼ���ϵ����㣬�� ��
A. ��x1��x2��1����y1-y2��+2a��x1-x2����0
B. ��1��x1��x2����y1-y2��+2a��x1-x2����0
C. ��x1��x2��1����y1-y2��+a��x1-x2����0
D. ��1��x1��x2����y1-y2��+a��x1-x2����0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com