
【题目】如图,在△ABC中,BA=BC,CD和BE是△ABC的两条高,∠BCD=45°,BE与CD交于点H.

(1)求证:△BDH≌△CDA;
(2)求证:BH=2AE.
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下10个乘积,回答问题:
11×29;12×28;13×27;14×26;15×25;16×24;17×23;18×22;19×21;20×20.
(1)将以上各乘积分别写成“a2﹣b2”(两数平方)的形式,将以上10个乘积按照从小到大的顺序排列起来;
(2)用含有a,b的式子表示(1)中的一个一般性的结论(不要求证明);
(3)根据(2)中的一般性的结论回答下面问题:某种产品的原料提价,因而厂家决定对产品进行提价,现有两种方案方案:第一次提价p%,第二次提价q%;方案2:第一、二次提价均为![]() %,其中p≠q,比较哪种方案提价最多?
%,其中p≠q,比较哪种方案提价最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
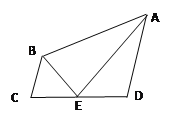
①BC+AD=AB ; ②E为CD中点
③∠AEB=90°; ④S△ABE=![]() S四边形ABCD
S四边形ABCD
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
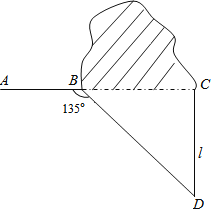
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
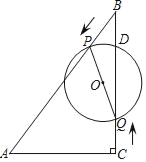
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,∠ABC=30°,动点P从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
(1)当t=1时,求△BPQ的面积;
(2)设⊙O的面积为y,求y与t的函数解析式;
(3)若⊙O与Rt△ABC的一条边相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m,宽为2m的长方形纸片,用剪刀沿图中虚线剪成四块形状大小完全一样的小长方形纸片,然后按图2的方式拼成1个空心正方形.(阴影部分为空心)
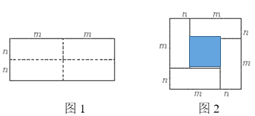
(1)请你用两种方法求图2中阴影部分的面积,直接用含m,n的代数式表示;方法① ;方法② .
(2)观察图2,请你写出![]()
![]() ,
,![]() 三个代数式之间存在的恒等关系式;
三个代数式之间存在的恒等关系式;
(3)已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com