
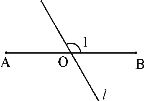
【题目】如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点。当△APB为直角三角形时,AP= .
【答案】3或3![]() 或3
或3![]() .
.
【解析】
试题分析:分以一下情况讨论:
(1)在Rt△A P1B中,∵∠1=120°,O P1=OB,∴∠O B P1 =∠O P1B=30°,∴AP1 =![]() AB=
AB=![]() ×6=3;
×6=3;
(2)在Rt△A P2B中,∵∠1=120°,O P2=OB,∴∠P2 B O =∠O P2B=60°,∴AP2 =![]() AB=cos∠O B P2×6=
AB=cos∠O B P2×6=![]() ×6=3
×6=3![]() ;
;
(3)P3B为以B为切点的⊙O的切线,∵∠1=120°,O P2=OB,∴∠P2 B O =∠O P2B=60°,∴∠P3O B=60°,在Rt△O P3B中,∴BP3 =tan∠P3O B×3 =![]() ×3=3
×3=3![]() ;在Rt△A P3B中,AP3 =
;在Rt△A P3B中,AP3 =![]() =
=![]() =3
=3![]() ;
;
(4)P4B为以A为切点的⊙O的切线,∵∠1=120°,O P1=OA,∴∠P1 A O =∠O P1A=60°,∴∠P4O A=60°,在Rt△O P4A中,∴AP4 =tan∠P4O A×3 =![]() ×3=3
×3=3![]() .
.
综上,当△APB为直角三角形时,AP=3,或3![]() ,或3
,或3![]() .
.



 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】(1)如果![]() =0,求[(x2+y2)+2y(x-y)-(x-y)(x+3y)]÷4y的值.
=0,求[(x2+y2)+2y(x-y)-(x-y)(x+3y)]÷4y的值.
(2)先化简,再求值:(2+a)(2-a)+a(a-5b)+3a5b3÷(-a2b)2,其中ab=-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省2014年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展, 2016年的快递业务量达到4.5亿件.设2015年与2016年这两年的平均增长率为x,则下列方程正确的是( )
A. 1.4(1+x)=4.5 B. 1.4(1+2x)=4.5
C. 1.4(1+x)2=4.5 D. 1.4(1+x)+1.4(1+x)2=4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动﹣旋转变换
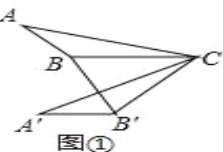
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com