
【题目】数学活动﹣旋转变换
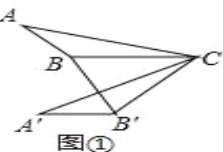
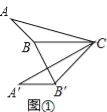
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
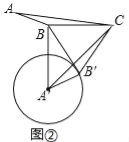
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
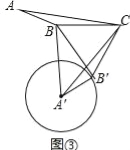
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
【答案】(1)65°;(2)切线;证明过程见解析;![]() ;(3)当α+β=180°时,直线BB′、是⊙A′的切线;
;(3)当α+β=180°时,直线BB′、是⊙A′的切线;![]()
【解析】
试题分析:(1)根据∠A′B′B=∠A′B′C﹣∠BB′C,只要求出∠A′B′B即可;(2)(Ⅰ)结论:直线BB′、是⊙A′的切线.只要证明∠A′B′B=90°即可.(Ⅱ)在RT△ABB′中,利用勾股定理计算即可;(3)如图③中,当α+β=180°时,直线BB′、是⊙A′的切线.只要证明∠A′B′B=90°即可解决问题.在△CBB′中求出BB′,再在RT△A′B′B中利用勾股定理即可.
试题解析:(1)如图①中,∵△A′B′C是由△ABC旋转得到, ∴∠A′B′C=∠ABC=130°,CB=CB′,
∴∠CBB′=∠CB′B,∵∠BCB′=50°, ∴∠CBB′=∠CB′B=65°,
∴∠A′B′B=∠A′B′C﹣∠BB′C=65°.
(2)(Ⅰ)结论:直线BB′、是⊙A′的切线.
理由:如图②中,∵∠A′B′C=∠ABC=150°,CB=CB′, ∴∠CBB′=∠CB′B,∵∠BCB′=60°,
∴∠CBB′=∠CB′B=60°, ∴∠A′B′B=∠A′B′C﹣∠BB′C=90°. ∴AB′⊥BB′,
∴直线BB′、是⊙A′的切线.
(Ⅱ)∵在RT△ABB′中,∵∠AB′B=90°,BB′=BC=5,AB′=AB=3,
∴A′B=![]() =
=![]() .
.
(3)如图③中,当α+β=180°时,直线BB′、是⊙A′的切线.
理由:∵∠A′B′C=∠ABC=α,CB=CB′, ∴∠CBB′=∠CB′B,∵∠BCB′=2β,
∴∠CBB′=∠CB′B=![]() , ∴∠A′B′B=∠A′B′C﹣∠BB′C=α﹣90°+β=180°﹣90°=90°.
, ∴∠A′B′B=∠A′B′C﹣∠BB′C=α﹣90°+β=180°﹣90°=90°.
∴AB′⊥BB′, ∴直线BB′、是⊙A′的切线. 在△CBB′中∵CB=CB′=n,∠BCB′=2β,
∴BB′=2nsinβ, 在RT△A′BB′中,A′B=![]() =
=![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】已知一个数为三位数,十位数字是a,个位数字比a小2,百位数字是a的2倍,则这个三位数可表示:( )
A. 21a-2 B. 211a-2 C. 200a-2 D. 3a-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某学校开展“远是君山,磨砺意志,保护江豚,爱鸟护鸟”为主题的远足活动.已知学校与君山岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
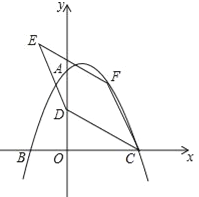
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com