
ЁОЬтФПЁПШчЭМЃЌ![]() гы
гы![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() гы
гы![]() жиКЯЃЌ
жиКЯЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌдђЯпЖЮ
ЕФжаЕуЃЌдђЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ ЃЌ
ЕФЪ§СПЙиЯЕЪЧ ЃЌ![]() гы
гы![]() ЕФЮЛжУЪЧ ЃЎ
ЕФЮЛжУЪЧ ЃЎ
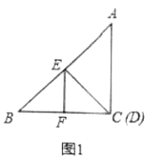
ЃЈ2ЃЉШчЭМ2ЃЌдкЭМ1ЕФЛљДЁЩЯЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЕНШчЭМ2ЕФЮЛжУЃЌЦфжа
ЫГЪБеыа§зЊЕНШчЭМ2ЕФЮЛжУЃЌЦфжа![]() дквЛЬѕжБЯпЩЯЃЌ
дквЛЬѕжБЯпЩЯЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌдђЯпЖЮ
ЕФжаЕуЃЌдђЯпЖЮ![]() гы
гы![]() ЪЧЗёДцдкФГжжШЗЖЈЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПжЄУїФуЕФНсТлЃЎ
ЪЧЗёДцдкФГжжШЗЖЈЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПжЄУїФуЕФНсТлЃЎ
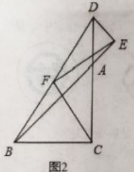
ЃЈ3ЃЉШє![]() ШЦ
ШЦ![]() Еуа§зЊШЮвтвЛИіНЧЖШЕНШчЭМ3ЕФЮЛжУЃЌ
Еуа§зЊШЮвтвЛИіНЧЖШЕНШчЭМ3ЕФЮЛжУЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧыФуЭъГЩЭМ3ЃЌВТЯыЯпЖЮ
ЃЌЧыФуЭъГЩЭМ3ЃЌВТЯыЯпЖЮ![]() гы
гы![]() ЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
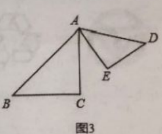
ЁОД№АИЁПЃЈ1ЃЉEF=FCЃЌEFЁЭFCЃЛЃЈ2ЃЉEF=FCЃЌEFЁЭFCЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉEF=FCЃЌEFЁЭFCЃЌжЄУїМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЕУГіЁїEFCЪЧЕШбќжБНЧШ§НЧаЮМДПЩЃЎ
ЃЈ2ЃЉбгГЄЯпЖЮCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂECЃЌРћгУSASжЄЁїBFCЁеЁїDFMЃЌНјЖјПЩвджЄУїЁїMDEЁеЁїCAEЃЌМДПЩЕУжЄЃЛ
ЃЈ3ЃЉбгГЄЯпЖЮCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂECЃЌРћгУSASжЄЁїBFCЁеЁїDFMЃЌНјЖјПЩвджЄУїЁїMDEЁеЁїCAEЃЌМДПЩЕУжЄЃЛЃЎ
НтЃКЃЈ1ЃЉЁп![]() гы
гы![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЁрBE=EC
Ёп![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃКEF=FCЃЌEFЁЭFC
ЃЈ2ЃЉДцдкEF=FCЃЌEFЁЭFCЃЌжЄУїШчЯТЃК
бгГЄCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂEC
Ёп![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрDF=FBЃЌ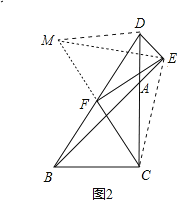
ЁпFC=FMЃЌЁЯBFC=ЁЯDFMЃЌDF=FBЃЌ
ЁрЁїBFCЁеЁїDFMЃЌ
ЁрDM=BCЃЌЁЯMDB=ЁЯFBCЃЌ
ЁрMD=ACЃЌMDЁЮBCЃЌ
ЁрЁЯMDC=ЁЯACB=90Ёу
ЁрЁЯMDE=ЁЯEAC=135ЁуЃЌ
ЁпED=EAЃЌ
ЁрЁїMDEЁеЁїCAEЃЈSASЃЉЃЌ
ЁрME=ECЃЌЁЯMED=ЁЯCEAЃЌ
ЁрЁЯMED+ЁЯFEA=ЁЯFEA+ЁЯCEA=90ЁуЃЌ
ЁрЁЯMEC=90ЁуЃЌгжFЮЊCMЕФжаЕуЃЌ
ЁрEF=FCЃЌEFЁЭFCЃЛ
ЃЈ3ЃЉEF=FCЃЌEFЁЭFCЃЎ
жЄУїШчЯТЃК
ШчЭМ4ЃЌбгГЄCFЕНMЃЌЪЙCF=FMЃЌСЌНгMEЁЂECЃЌСЌНгDMНЛбгГЄНЛAEгкGЃЌНЛACгкHЃЌ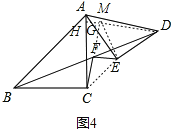
ЁпFЮЊBDжаЕуЃЌ
ЁрDF=FBЃЌ
дкЁїBCFКЭЁїDFMжа
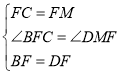
ЁрЁїBFCЁеЁїDFMЃЈSASЃЉЃЌ
ЁрDM=BCЃЌЁЯMDB=ЁЯFBCЃЌ
ЁрMD=ACЃЌspan>HDЁЮBCЃЌ
ЁрЁЯAHG=ЁЯBCA=90ЁуЃЌЧвЁЯAGH=ЁЯDGEЃЌ
ЁрЁЯMDE=ЁЯEACЃЌ
дкЁїMDEКЭЁїCAEжа
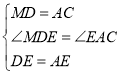
ЁрME=ECЃЌЁЯMED=ЁЯCEAЃЌ
ЁрЁЯMED+ЁЯFEA=ЁЯFEA+ЁЯCEA=90ЁуЃЌ
ЁрЁЯMEC=90ЁуЃЌгжFЮЊCMЕФжаЕуЃЌ
ЁрEF=FCЃЌEFЁЭFCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЩњВњЕФФГжжВњЦЗАДжЪСПЗжЮЊ![]() ИіЕЕДЮЃЌЩњВњЕквЛЕЕДЮЃЈМДзюЕЭЕЕДЮЃЉЕФВњЦЗвЛЬьЩњВњ
ИіЕЕДЮЃЌЩњВњЕквЛЕЕДЮЃЈМДзюЕЭЕЕДЮЃЉЕФВњЦЗвЛЬьЩњВњ![]() МўЃЌУПМўРћШѓ
МўЃЌУПМўРћШѓ![]() дЊЃЌУПЬсИпвЛИіЕЕДЮЃЌРћШѓУПМўдіМг
дЊЃЌУПЬсИпвЛИіЕЕДЮЃЌРћШѓУПМўдіМг![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉУПМўРћШѓЮЊ![]() дЊЪБЃЌДЫВњЦЗжЪСПдкЕкМИЕЕДЮЃП
дЊЪБЃЌДЫВњЦЗжЪСПдкЕкМИЕЕДЮЃП
ЃЈ2ЃЉгЩгкЩњВњЙЄађВЛЭЌЃЌДЫВњЦЗУПЬсИпвЛИіЕЕДЮЃЌвЛЬьВњСПМѕЩй![]() МўЃЎШєЩњВњЕк
МўЃЎШєЩњВњЕк![]() ЕЕЕФВњЦЗвЛЬьЕФзмРћШѓЮЊ
ЕЕЕФВњЦЗвЛЬьЕФзмРћШѓЮЊ![]() дЊЃЈЦфжа
дЊЃЈЦфжа![]() ЮЊе§ећЪ§ЃЌЧв
ЮЊе§ећЪ§ЃЌЧв![]() Ём
Ём![]() Ём
Ём![]() ЃЉ,ЧѓГі
ЃЉ,ЧѓГі![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛШєЩњВњФГЕЕДЮВњЦЗвЛЬьЕФзмРћШѓЮЊ
ЕФКЏЪ§ЙиЯЕЪНЃЛШєЩњВњФГЕЕДЮВњЦЗвЛЬьЕФзмРћШѓЮЊ![]() дЊЃЌИУЙЄГЇЩњВњЕФЪЧЕкМИЕЕДЮЕФВњЦЗЃП
дЊЃЌИУЙЄГЇЩњВњЕФЪЧЕкМИЕЕДЮЕФВњЦЗЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌвбжЊAB=ACЃЌЁЯBAC=90ЁуЃЌEЮЊБпACЩЯвЛЕуЃЌСЌНгBEЃЎ
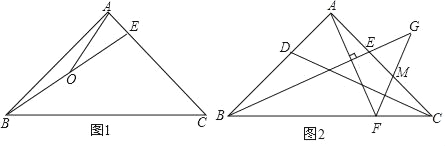
(1)ШчЭМ1ЃЌШєЁЯABE=15ЁуЃЌOЮЊBEжаЕуЃЌСЌНгAOЃЌЧвAO=1ЃЌЧѓBCЕФГЄЃЛ
(2)ШчЭМ2ЃЌDЮЊABЩЯвЛЕуЃЌЧвТњзуAE=ADЃЌЙ§ЕуAзїAFЁЭBEНЛBCгкЕуFЃЌЙ§ЕуFзїFGЁЭCDНЛBEЕФбгГЄЯпгкЕуGЃЌНЛACгкЕуMЃЌЧѓжЄЃКBG=AF+FGЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
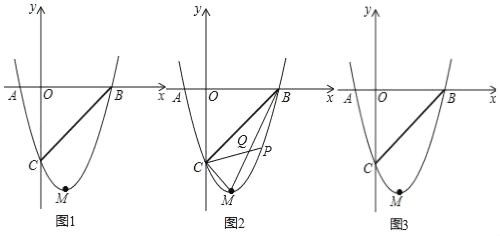
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=mx2Љ2mxЉ3mЃЈmЃО0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуMЮЊХзЮяЯпЕФЖЅЕуЃЌЧвOC=OBЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєХзЮяЯпЩЯгавЛЕуPЃЌСЌPCНЛЯпЖЮBMгкQЕуЃЌЧвSЁїBPQ=SЁїCMQЃЌЧѓPЕуЕФзјБъЃЎ
ЃЈ3ЃЉАбХзЮяЯпбиxжсе§АыжсЦНвЦnИіЕЅЮЛЃЌЪЙЦНвЦКѓЕФХзЮяЯпНЛжБЯпBCгкEЁЂFСНЕуЃЌЧвEЁЂFЙигкЕуBЖдГЦЃЌЧѓnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГѕШ§ЃЈ1ЃЉАрвЊДг2Фа2ХЎЙВ4УћЭЌбЇжабЁШЫзіГПЛсЕФЩ§ЦьЪжЃЎ
ЃЈ1ЃЉШєДгет4ШЫжаЫцЛњбЁ1ШЫЃЌдђЫљбЁЕФЭЌбЇадБ№ЮЊФаЩњЕФИХТЪЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєДгет4ШЫжаЫцЛњбЁ2ШЫЃЌЧѓет2УћЭЌбЇадБ№ЯрЭЌЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЪЕЪ§aЃЌbЃЌЮвУЧПЩвдгУmin{aЃЌb}БэЪОaЃЌbСНЪ§жаНЯаЁЕФЪ§ЃЌР§Шчmin{3ЃЌЃ1}ЃНЃ1ЃЌmin{2ЃЌ2}ЃН2. РрЫЦЕиЃЌШєКЏЪ§y1ЁЂy2ЖМЪЧxЕФКЏЪ§ЃЌдђyЃНmin{y1ЃЌ y2}БэЪОКЏЪ§y1КЭy2ЕФЁАШЁаЁКЏЪ§ЁБЃЎ
ЃЈ1ЃЉЩшy1ЃНxЃЌy2ЃН![]() ЃЌдђКЏЪ§yЃНmin{xЃЌ
ЃЌдђКЏЪ§yЃНmin{xЃЌ ![]() }ЕФЭМЯёгІИУЪЧ жаЕФЪЕЯпВПЗжЃЎ
}ЕФЭМЯёгІИУЪЧ жаЕФЪЕЯпВПЗжЃЎ

ЃЈ2ЃЉЧыдкЯТЭМжагУДжЪЕЯпУшГіКЏЪ§yЃНmin{(xЃ2)2ЃЌ (xЃЋ2)2}ЕФЭМЯёЃЌВЂаДГіИУЭМЯёЕФШ§ЬѕВЛЭЌаджЪЃК

Ђй ЃЛ
Ђк ЃЛ
Ђл ЃЛ
ЃЈ3ЃЉКЏЪ§yЃНmin{(xЃ4)2ЃЌ (xЃЋ2)2}ЕФЭМЯёЙигк ЖдГЦЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
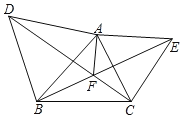
ЁОЬтФПЁПШчЭМЃЌЗжБ№вдЁїABCЕФБпABЃЌACЯђЭтзїСНИіЕШБпШ§НЧаЮЁїABDЃЌЁїACEЃЎСЌНгBEЁЂCDНЛЕуFЃЌСЌНгAFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁеЁїAEBЃЛ
ЃЈ2ЃЉЧѓжЄЃКAF+BF+CF=CDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
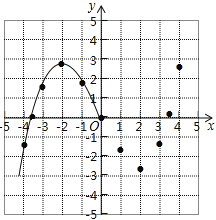
ЁОЬтФПЁПФГбЇЯАаЁзщдкбаОПКЏЪ§y=![]() x3Љ2xЕФЭМЯѓгыаджЪЪБЃЌвбСаБэЁЂУшЕуВЂЛГіСЫЭМЯѓЕФвЛВПЗжЃЎ
x3Љ2xЕФЭМЯѓгыаджЪЪБЃЌвбСаБэЁЂУшЕуВЂЛГіСЫЭМЯѓЕФвЛВПЗжЃЎ
x | Ё | Љ4 | Љ3.5 | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | 3.5 | 4 | Ё |
y | Ё | Љ | Љ |
|
|
| 0 | Љ | Љ | Љ |
|
| Ё |
ЃЈ1ЃЉЧыВЙШЋКЏЪ§ЭМЯѓЃЛ
ЃЈ2ЃЉЗНГЬ![]() x3Љ2x=Љ2ЪЕЪ§ИљЕФИіЪ§ЮЊЁЁ ЁЁЃЛ
x3Љ2x=Љ2ЪЕЪ§ИљЕФИіЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉЙлВьЭМЯѓЃЌаДГіИУКЏЪ§ЕФСНЬѕаджЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
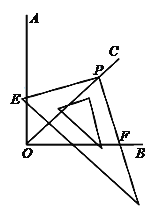
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=90ЁуЃЌНЋШ§НЧГпЕФжБНЧЖЅЕуPТфдкЁЯAOBЕФЦНЗжЯпOCЕФШЮвтвЛЕуЩЯЃЌЪЙШ§НЧГпЕФСНЬѕжБНЧБпгыЁЯAOBЕФСНБпЗжБ№ЯрНЛгкЕуEЁЂFЁЃжЄУїЃКPE=PFЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com