
【题目】若关于x的方程x2+2(m﹣1)x+m2﹣2m﹣3=0(m为实数).
(1)求证:不论m为何值,该方程均有两个不等的实根;
(2)解方程求出两个根x1,x2(x1>x2),并求w=x1(x1+x2)+x12的最值.
【答案】(1)见解析;(2)-![]() .
.
【解析】
(1)根据b2﹣4ac与零的关系即可判断出的关于x的一元二次方程mx2﹣3(m﹣1)x+2m﹣3=0(m为实数)的根的情况;
(2)用因式分解法求得方程的两个根,代入w中,化简并配方可得最小值.
(1)△=[2(m﹣1)]2﹣4×1×(m2﹣2m﹣3)=16>0,∴不论m为何值,该方程均有两个不等的实根;
(2)x2+2(m﹣1)x+m2﹣2m﹣3=0,(x+m﹣3)(x+m+1)=0.
∵x1>x2,∴x1=﹣m+3,x2=﹣m﹣1,∴w=x1(x1+x2)+![]() =(﹣m+3)(﹣2m+2)+(﹣m+3)2=3m2﹣14m+15=3(m﹣
=(﹣m+3)(﹣2m+2)+(﹣m+3)2=3m2﹣14m+15=3(m﹣![]() )2﹣
)2﹣![]() .
.
∵3>0,∴w有最小值是﹣![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+mx+n经过点A(﹣1,0)和B(0,3).
(1)求抛物线的表达式;
(2)抛物线与x轴的正半轴交于点C,连接BC.设抛物线的顶点P关于直线y=t的对称点为点Q,若点Q落在△OBC的内部,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
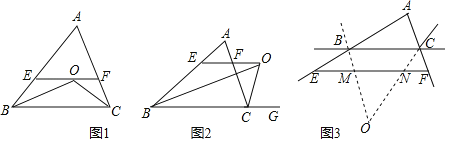
【题目】已知,如图1:![]() 中,
中,![]() 、
、![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]()
(1)直接写出图1中所有的等腰三角形.指出![]() 与
与![]() 、
、![]() 间有怎样的数量关系?
间有怎样的数量关系?
(2)在(1)的条件下,若![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
(3)如图2,若![]() 中,
中,![]() 的平分线与三角形外角
的平分线与三角形外角![]() 的平分线
的平分线![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,请问(1)中
,请问(1)中![]() 与
与![]() 、
、![]() 间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
(4)如图3,![]() 、
、![]() 的外角平分线的延长线相交于点
的外角平分线的延长线相交于点![]() ,请直接写出
,请直接写出![]() ,
,![]() 、
、![]() ,
,![]() 之间的数量关系.不需证明.
之间的数量关系.不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
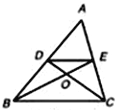
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 在平面直角坐标系中与
在平面直角坐标系中与![]() 轴交于点A,点B(-3,3)也在直线
轴交于点A,点B(-3,3)也在直线![]() 上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线
上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线![]() 上.
上.
(1)求点C的坐标和直线![]() 的解析式;
的解析式;
(2)已知直线![]() :
:![]() 经过点B,与
经过点B,与![]() 轴交于点E,求△ABE的面积.
轴交于点E,求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
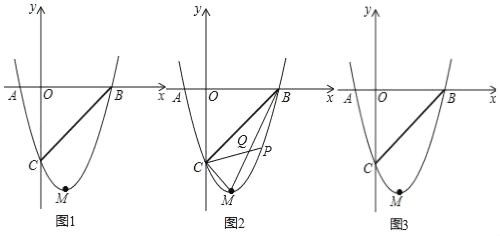
【题目】如图,抛物线y=mx2﹣2mx﹣3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com