
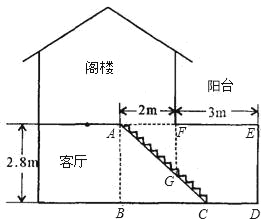
ЁОЬтФПЁПЭєРЯЪІвЊзАаоздМКДјИѓТЅЕФаТОгЃЈЯТЭМЮЊаТОгЦЪУцЭМЃЉЃЌдкНЈдьПЭЬќЕНИѓТЅЕФТЅЬнACЪБЃЌЮЊБмУтЩЯТЅЪБЧННЧFХіЭЗЃЌЩшМЦЧННЧFЕНТЅЬнЕФЪњжБОрРыFGЮЊ1.75mЃЎЫћСПЕУПЭЬќИпAB=2.8mЃЌТЅЬнЖДПкПэAF=2mЃЎИѓТЅбєЬЈПэEF=3mЃЎЧыФуАяжњЭєРЯЪІНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉвЊЪЙЧННЧFЕНТЅЬнЕФЪњжБОрРыFGЮЊ1.75mЃЌТЅЬнЕзЖЫCЕНЧННЧDЕФОрРыCDЪЧЖрЩйУзЃП
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЮЊБЃжЄЩЯТЅЪБЕФЪцЪЪИаЃЌТЅЬнЕФУПИіЬЈНзаЁгк20cmЃЌУПИіЬЈНзПэвЊДѓгк20cmЃЌЮЪЭєРЯЪІгІИУНЋТЅЬнНЈМИИіЬЈНзЃПЮЊЪВУДЃП
ЁОД№АИЁПЃЈ1ЃЉCD=1.8mЃЛЃЈ2ЃЉТЅЬнгІНЈ15ИіЬЈНзЃЌРэгЩЯъМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉБОЬтЮЊзлКЯадЪЕМЪгІгУЬтЃЌДЫРрЬтФПвЊШЯецЗжЮіЫљИјЬѕМўЃЌЗЂЯжЁїABCЁзЁїGFAЃЌДгЖјПЩЧѓГіCDЕФжЕ;ЃЈ2ЃЉПЩгЩЬтвтСаВЛЕШЪННтОіЮЪЬтЃЎжаПМжаЙигкЪЕМЪОМУЩњЛюЕФгІгУЬтЮЊвЛДѓШШЕуЃЌЬтФПЮФзжЖрЃЌЪ§ОнЖрЁЂЪ§СПЙиЯЕЖрЃЌвђДЫРэНтЬтвтЃЌСаГіВЛЕШЪНЁЂЗНГЬЪЧЙиМќЃЌЭљЭљашвЊдкИјГіЕФЮЪЬтжаЩшМЦВЛЭЌЕФЗНАИЃЌНјЖјБШНЯдёгХЃЌбАЧѓзюМбЗНАИЃЎ
ЃЈ1ЃЉИљОнЬтвтгаAFЁЮBC
ЁрЁЯACB=ЁЯGAFЃЌ
гжЁЯABC=ЁЯAFG=90Ёу
ЁрЁїABCЁзЁїGFAЃЎ
Ёр![]() ,
,
МД![]() ЃЌ
ЃЌ
ЕУBC=3.2ЃЈmЃЉ
CD=ЃЈ2+3ЃЉЉ3.2=1.8ЃЈmЃЉЃЎ
ЃЈ2ЃЉЩшТЅЬнгІНЈnИіЬЈНзЃЌдђ![]() ,
,
НтЕУ14ЃМnЃМ16ЃЎ
ЁпnЪЧећЪ§ЃЌ
ЁрТЅЬнгІНЈ15ИіЬЈНзЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕБx1=aЁЂx2=bЁЂx3=cЪБЃЌЖўДЮКЏЪ§y=Љ![]() x2+kxЖдгІЕФКЏЪ§жЕЗжБ№ЮЊy1ЁЂy2ЁЂy3ЃЌШєе§ећЪ§aЁЂbЁЂcЧЁКУЪЧвЛИіШ§НЧаЮЕФШ§БпГЄЃЌЧвЕБaЃМbЃМcЪБЃЌЖМгаy1ЃОy2ЃОy3ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
x2+kxЖдгІЕФКЏЪ§жЕЗжБ№ЮЊy1ЁЂy2ЁЂy3ЃЌШєе§ећЪ§aЁЂbЁЂcЧЁКУЪЧвЛИіШ§НЧаЮЕФШ§БпГЄЃЌЧвЕБaЃМbЃМcЪБЃЌЖМгаy1ЃОy2ЃОy3ЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаФРэбЇМвбаОПЗЂЯжЃЌвЛАуЧщПіЯТЃЌвЛНкПЮ40ЗжжгжаЃЌбЇЩњЕФзЂвтСІЫцНЬЪІНВПЮЕФБфЛЏЖјБфЛЏЃЎПЊЪМЩЯПЮЪБЃЌбЇЩњЕФзЂвтСІж№ВНдіЧПЃЌжаМфгавЛЖЮЪБМфбЇЩњЕФзЂвтСІБЃГжНЯЮЊРэЯыЕФЮШЖЈзДЬЌЃЌЫцКѓбЇЩњЕФзЂвтСІПЊЪМЗжЩЂЃЎОЙ§ЪЕбщЗжЮіПЩжЊЃЌбЇЩњЕФзЂвтСІжИЪ§yЫцЪБМфxЃЈЗжжгЃЉЕФБфЛЏЙцТЩШчЯТЭМЫљЪОЃЈЦфжаABЁЂBCЗжБ№ЮЊЯпЖЮЃЌCDЮЊЫЋЧњЯпЕФвЛВПЗжЃЉЃК
ЃЈ1ЃЉЧѓГіЯпЖЮABЃЌЧњЯпCDЕФНтЮіЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉПЊЪМЩЯПЮКѓЕкЮхЗжжгЪБгыЕкШ§ЪЎЗжжгЪБЯрБШНЯЃЌКЮЪБбЇЩњЕФзЂвтСІИќМЏжаЃП
ЃЈ3ЃЉвЛЕРЪ§бЇОКШќЬтЃЌашвЊНВ19ЗжжгЃЌЮЊСЫаЇЙћНЯКУЃЌвЊЧѓбЇЩњЕФзЂвтСІжИЪ§зюЕЭДяЕН36ЃЌФЧУДОЙ§ЪЪЕБАВХХЃЌРЯЪІФмЗёдкбЇЩњзЂвтСІДяЕНЫљашЕФзДЬЌЯТНВНтЭъетЕРЬтФПЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDжаЃЌEЪЧCDбгГЄЯпЩЯвЛЕуЃЌBEгыADНЛгкЕуFЃЌCD=2DEЃЌШєЁїDEFЕФУцЛ§ЮЊaЃЌдђABCDЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
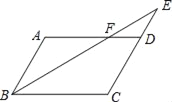
A. 6a B. 8a C. 9a D. 12a
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЯТСаЗНГЬЃК
ЃЈ1ЃЉx2+4xЉ5=0
ЃЈ2ЃЉЃЈ3xЉ2ЃЉ2=4ЃЈ3ЉxЃЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЛлЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъГЩЃК
ЃЈ1ЃЉКЏЪ§![]() ЕФздБфСП
ЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЪЧ______________ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ______________ЃЛ
ЃЈ2ЃЉСаБэЃЌевГі![]() гы
гы![]() ЕФМИзщЖдгІжЕЃЎ
ЕФМИзщЖдгІжЕЃЎ
x | Ё | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё | b | 1 | 0 | 1 | 2 | Ё |
ЦфжаЃЌ![]() ______________ЃЛ
______________ЃЛ
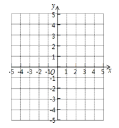
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГівдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌВЂЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
жаЃЌУшГівдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌВЂЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉКЏЪ§y=|xЉ1|ЕФзюаЁжЕЮЊ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЙигквЛДЮКЏЪ§:![]() ЕФЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
ЕФЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
A.ЫќЕФЭМЯѓгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЪЧ![]()
B.Еу![]() дкетИіКЏЪ§ЕФЭМЯѓЩЯ
дкетИіКЏЪ§ЕФЭМЯѓЩЯ
C.ЫќЕФКЏЪ§жЕ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁ
ЕФдіДѓЖјМѕаЁ
D.ЫќЕФЭМЯѓОЙ§ЕквЛЁЂЖўЁЂШ§ЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁбOЪЧе§ЗНаЮABCDЕФЭтНгдВЃЌPЪЧЁбOЩЯВЛгыAЁЂBжиКЯЕФШЮвтвЛЕуЃЌдђЁЯAPBЕШгкЃЈ ЃЉ
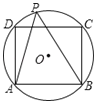
AЃЎ45Ёу BЃЎ60Ёу CЃЎ45Ёу Лђ135Ёу DЃЎ60Ёу Лђ120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇКмПсЃЌШУЮвУЧгУРэадЫМЮЌетвЛРћЦїЃЌШЅвЛМИКЮЕФФЇЗЈЪРНчАЩЃЎЧыАДвЊЧѓЃЌЭъГЩЯТУцЕФЛцЭМЃКзїЭМвЊЧѓЃКЂйНіЪЙгУЮоПЬЖШжБГпЃКЂквЊЙЙдьЕФЕуБиаыЪЧИёЕуЃЎ
ОпЬхвЊЧѓЃК
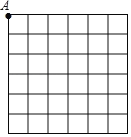
ЃЈ1ЃЉдкШчЭМ6ЁС6ЭјИёжаЃЌЙЙдьЫљгаЕШбќШ§НЧаЮЃЌЦфжаИіЕуЮЊAЃЌЧввЛЬѕБпГЄЮЊ![]() ЃЛЗћКЯЬѕМўЕФШ§НЧаЮгаЁЁЁЁЁЁЁЁ ИіЃЌдкЭМЩЯБъГіЃЎ
ЃЛЗћКЯЬѕМўЕФШ§НЧаЮгаЁЁЁЁЁЁЁЁ ИіЃЌдкЭМЩЯБъГіЃЎ
ЃЈ2ЃЉМђЪіЙЙдьГЄЖШЮЊ![]() ЕФЯпЖЮЕФРэТлвРОнМАМЦЫуЙ§ГЬЃЎ
ЕФЯпЖЮЕФРэТлвРОнМАМЦЫуЙ§ГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com