
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

【答案】(1)AB解析式为:y1=2x+20(0≤x≤10).曲线CD的解析式为:y2=![]() (x≥25);(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
(x≥25);(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
【解析】
(1)利用待定系数法分别求出AB和CD的函数表达式,进而得出答案;
(2)利用(1)中所求解析式,计算出第五分钟和第三十分钟的注意力指数,最后比较判断;
(3)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.
(1)设线段AB所在的直线的解析式为y1=k1x+20,
把B(10,40)代入得,k1=2,
∴AB解析式为:y1=2x+20(0≤x≤10).
设C、D所在双曲线的解析式为y2=![]() ,
,
把C(25,40)代入得,k2=1000,
∴曲线CD的解析式为:y2=![]() (x≥25);
(x≥25);
(2)当x1=5时,y1=2×5+20=30,
当x2=30时,y2=![]() ,
,
∴y1<y2
∴第30分钟注意力更集中.
(3)令y1=36,
∴36=2x+20,
∴x1=8
令y2=36,
∴36=![]() ,
,
∴x2=![]() ≈27.8,
≈27.8,
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x–2)(x–3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是
A. 当m=0时,x1=2,x2=3
B. m>–![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x–x1)(x–x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2…An﹣1为OA的n等分点,点B1,B2…Bn﹣1为CB的n等分点,连结A1B1,A2B2,…An﹣1Bn﹣1,分别交曲线![]() (x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)
(x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数( )
①近似数![]() 精确到十分位:
精确到十分位:
②在![]() ,
,![]() ,
,![]() ,
,![]() 中,最小的数是
中,最小的数是![]()
③如图①所示,在数轴上点![]() 所表示的数为
所表示的数为![]()
④反证法证明命题“一个三角形中最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”
⑤如图②,在![]() 内一点
内一点![]() 到这三条边的距离相等,则点
到这三条边的距离相等,则点![]() 是三个角平分线的交点
是三个角平分线的交点
图① 图②
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+mx+n经过点A(﹣1,0)和B(0,3).
(1)求抛物线的表达式;
(2)抛物线与x轴的正半轴交于点C,连接BC.设抛物线的顶点P关于直线y=t的对称点为点Q,若点Q落在△OBC的内部,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
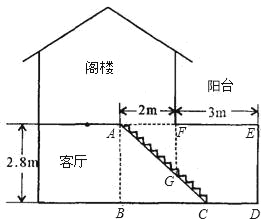
【题目】汪老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m.阁楼阳台宽EF=3m.请你帮助汪老师解决下列问题:
(1)要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米?
(2)在(1)的条件下,为保证上楼时的舒适感,楼梯的每个台阶小于20cm,每个台阶宽要大于20cm,问汪老师应该将楼梯建几个台阶?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com