
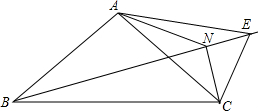
 ��ͼ���ڡ�ABC�У�AB=AC����ABC=��������B��һֱ��l����l��ȡ��E��ʹAE=AC������CE����CAE��ƽ���߽�BE�ڵ�N������NC��
��ͼ���ڡ�ABC�У�AB=AC����ABC=��������B��һֱ��l����l��ȡ��E��ʹAE=AC������CE����CAE��ƽ���߽�BE�ڵ�N������NC������ ��1����BN�Ͻ�ȡBF=CN������AF���ӳ�AN��CE��G�����ݵ��������ε����ʵõ�AG��ֱƽ��CE�����߶δ�ֱƽ���ߵ����ʵõ�CN=NE���Ƴ���NCE=��NEC������֪�����õ���ACE=��AEC�����������õ���ACN=��AEN��֤�á�ABF=��ACN���Ƴ���ABF�ա�ACN������ȫ�������ε����ʵõ�BF=CN��AF=AN����BAF=��CAN�����ǵõ���FAN=��BAC�����������ε��ڽǺ͵õ���FAN=��BAC=90�㣬���ǵõ����ۣ�
��2����ͼ2����BN�Ͻ�ȡBF=CN������AF���ӳ�AN��CE��G����A��AH��BE��H���ɣ�1��֤�á�FAN=��BAC�����������ε��ڽǺ͵õ���FAN=��BAC=180��-2��30��=120�㣬���ǵõ���AFH=��ANH=30�㣬�������Ǻ����õ�HN=$\frac{\sqrt{3}}{2}$AN�����FN=$\sqrt{3}$AN�����ǵõ����ۣ�
��3���ɣ�1��֤�á�FAN=��BAC���������ε��ڽǺ͵õ���FAN=��BAC=180��-2�������ǵõ���AFH=��ANH=�����������Ǻ����Ķ���õ�HN=ANcos�������ǵõ�FN=2ANcos�������ɵõ����ۣ�
��� �⣺��1��$\sqrt{2}$AN=BN-CN��
��BN�Ͻ�ȡBF=CN������AF���ӳ�AN��CE��G��
��AE=AC��ANƽ�֡�CAE��
��AG��ֱƽ��CE��
��CN=NE��
���NCE=��NEC��
��AC=AE��
���ACE=��AEC��
���ACN=��AEN��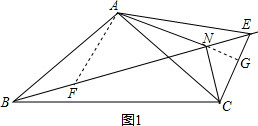
��AB=AC=AE��
���ABF=��AEB��
���ABF=��ACN��
�ڡ�ABF���ACN�У�
$\left\{\begin{array}{l}{AB=AC}\\{��ABF=��ACN}\\{BF=CN}\end{array}\right.$��
���ABF�ա�ACN��
��BF=CN��AF=AN����BAF=��CAN��
���FAN=��BAC��
�ߡ�ABC=45�㣬
���FAN=��BAC=90�㣬
��FN=$\sqrt{2}$AN��
��BN-BF=BN-CN=$\sqrt{2}$AN��
��$\sqrt{2}$AN=BN-CN��
�ʴ�Ϊ��$\sqrt{2}$AN=BN-CN��
��2������=30��ʱ��
��ͼ2��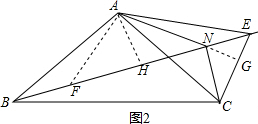 ��BN�Ͻ�ȡBF=CN������AF���ӳ�AN��CE��G����A��AH��BE��H��
��BN�Ͻ�ȡBF=CN������AF���ӳ�AN��CE��G����A��AH��BE��H��
�ɣ�1��֤�á�FAN=��BAC��
�ߦ�=30�㣬
���FAN=��BAC=180��-2��30��=120�㣬
���AFH=��ANH=30�㣬
��HN=$\frac{\sqrt{3}}{2}$AN��
��FN=$\sqrt{3}$AN��
��$\sqrt{3}$AN=BN-CN��
�ʴ�Ϊ��$\sqrt{3}$AN=BN-CN��
��3���ɣ�1��֤�á�FAN=��BAC��
���FAN=��BAC=180��-2��=��
���AFH=��ANH=����
��HN=ANcos����
��FN=2ANcos����
��2ANcos��=BN-CN��
��AN=$\frac{BN-CN}{2cos��}$��
�ʴ�Ϊ��AN=$\frac{BN-CN}{2cos��}$��
���� ���⿼����ȫ�������ε��ж������ʣ����������ε����ʣ�����ֱ�������ε����ʣ���ȷ�������������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
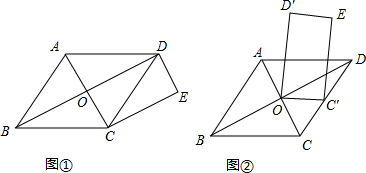
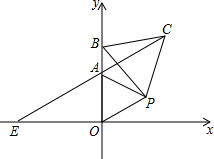 ��ͼ����ƽ��ֱ������ϵ�У���AOPΪ�ȱ������Σ�A������Ϊ��0��1������BΪy����λ��A���Ϸ���һ�����㣬��BPΪ����BP���Ҳ����ȱߡ�PBC������CA�����ӳ�CA��x���ڵ�E��
��ͼ����ƽ��ֱ������ϵ�У���AOPΪ�ȱ������Σ�A������Ϊ��0��1������BΪy����λ��A���Ϸ���һ�����㣬��BPΪ����BP���Ҳ����ȱߡ�PBC������CA�����ӳ�CA��x���ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
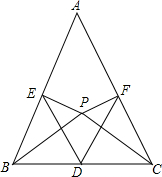 �ڡ�ABC�У�AB=AC��DΪBC�ߵ��е㣬���������ڲ�ȡһ��P��ʹ�á�ABP=��ACP������P��PE��AC�ڵ�E��PF��AB�ڵ�F��
�ڡ�ABC�У�AB=AC��DΪBC�ߵ��е㣬���������ڲ�ȡһ��P��ʹ�á�ABP=��ACP������P��PE��AC�ڵ�E��PF��AB�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
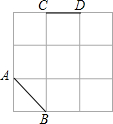 �����⣺��ͼ����3��3�����У���֪�߶�AB��CD���Ը��Ϊ�˵㻭һ���߶Σ�ʹ����AB��CD�����Գ�ͼ�Σ����������п��ܣ�
�����⣺��ͼ����3��3�����У���֪�߶�AB��CD���Ը��Ϊ�˵㻭һ���߶Σ�ʹ����AB��CD�����Գ�ͼ�Σ����������п��ܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ǷǸ��� | B�� | ���Ǹ��� | C�� | �������� | D�� | ������һ��Ϊ0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+y2 | B�� | -x2-y2 | C�� | x2+4xy+4y2 | D�� | x2+xy+y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�һ��ƻ���Ƿ��� | |
| B�� | ���ij�ֵ����ķ���뾶 | |
| C�� | ��������ѧ���ġ������������ࡱ����ʶ | |
| D�� | ��顰�϶�5�š�����������Ƿ�ϸ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com