
分析 (1)直接利用二次根式的除法运算法则化简求出即可;
(2)直接利用二次根式的除法运算法则化简求出即可.
解答 解:(1)$\sqrt{\frac{2{a}^{2}{b}^{2}}{{c}^{5}}}$÷(-$\sqrt{\frac{ab}{{c}^{3}}}$)
=-$\sqrt{\frac{2{a}^{2}{b}^{2}}{{c}^{5}}×\frac{{c}^{3}}{ab}}$
=-$\frac{\sqrt{2ab}}{c}$;
(2)-$\sqrt{1\frac{2}{3}}$÷$\sqrt{\frac{5}{54}}$
=-$\sqrt{\frac{5}{3}×\frac{54}{5}}$
=-3$\sqrt{3}$.
点评 此题主要考查了二次根式的乘除运算,正确化简二次根式是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | 2015 | D. | 1或0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
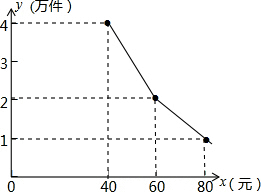 为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.
为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司的经营利润逐步偿还无息贷款,一盒子该产品的生产成本为每件40元;员工每人每月工资是2500元,公司每月支出其它费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系式如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com