
分析 先将关于x的二次多项式变形,根据二次多项式的特点求出a的值;再根据当x=2时,多项式的值为-26,求出b的值;进而求出当x=-2时,该多项式的值.
解答 解:a(x3-x2+3x)+b(2x2+x)+x3-5
=ax3-ax2+3ax+2bx2+bx+x3-5
=(a+1)x3+(2b-a)x2+(3a+b)x-5.
∵原式是二次多项式,
∴a+1=0,a=-1.
∴原式=(2b+1)x2+(b-3)x-5.
∵当x=2时,原式=10b-7=-26.
∴b=-1.9,
当x=-2时,原式=6b+5=-6.4.
点评 本题主要考查了二次多项式的特点.注意三次项不存在说明它们合并的结果为0,依此求得a的值是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
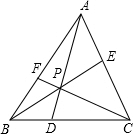 如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.
如图,在△ABC内任取一点P,连接并延长AP、BP、CP,分别交对边于点D、E、F,则$\frac{PD}{AD}$+$\frac{PE}{BE}$+$\frac{PF}{CF}$=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com