
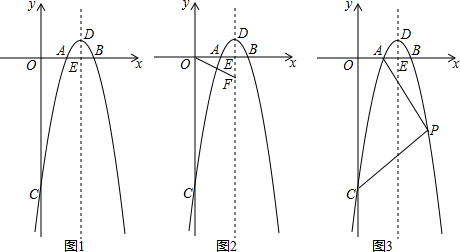
分析 (1)令y=-(x-2)(x-k)=0,则x1=2,x2=k,根据k>2,点A在点B的左侧可得出A、B两点的坐标,由AB=2可求出k的值,进而得出函数解析式;
(2)把函数解析式化为顶点式的形式可得出其顶点坐标与对称轴方程,过顶点D作DM⊥Oy,垂足为M,由OF⊥CD,∠FOE=∠OCD,由锐角三角函数的定义可求出EF的长,故可得出F点的坐标;
(3)由(1)知y=-x2+6x-8,A(2,0)、B(4,0),设P(m,-m2+6m-8),过点P作PN⊥Oy垂足为N,PG⊥Ox垂足为G,根据∠PAB=∠OCP可求出m的值,根据△PAG为等腰直角三角形可得出PH的长,由锐角三角函数的定义可得出结论.
解答 解:(1)∵令y=-(x-2)(x-k)=0,
∴x1=2,x2=k,
∵k>2,点A在点B的左侧,
∴A(2,0),B(k,0)
∵AB=2,
∴k-2=2,
∴k=4,
∴y=-(x-2)(x-4)=-x2+6x-8,
∴抛物线的解析式为y=-x2+6x-8.
(2)∵y=-(x-2)(x-k)=-x2+(k+2)x-2k=-(x-$\frac{k+2}{2}$)2+$\frac{(k-2)^{2}}{4}$
∴抛物线的顶点坐标为($\frac{k+2}{2}$,$\frac{{(k-2)}^{2}}{4}$),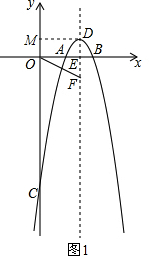
抛物线的对称轴为直线x=$\frac{k+2}{2}$.
如图1,过顶点D作DM⊥Oy,垂足为M,
∵OF⊥CD,
∴∠FOE=∠OCD,
tan∠COD=$\frac{DM}{MC}$=$\frac{OE}{MC}$=$\frac{OE}{\frac{(k-2)^{2}}{4}-(-2k)}$=$\frac{OE}{(\frac{k+2}{2})^{2}}$,
∴tan∠EOF=$\frac{EF}{OE}$,
∴$\frac{OE}{(\frac{k+2}{2})^{2}}$=$\frac{EF}{OE}$,
∴$\frac{\frac{k+2}{2}}{{(\frac{k+2}{2})}^{2}}$=$\frac{EF}{\frac{k+2}{2}}$,
∴EF=1,
∴F($\frac{k+2}{2}$,-1),
∴点F的纵坐标为-1;
(3)由(1)知y=-x2+6x-8,A(2,0)、B(4,0),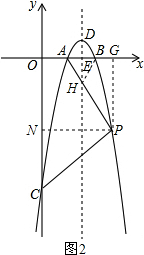 设P(m,-m2+6m-8),如图2,过点P作PN⊥Oy垂足为N,PG⊥Ox垂足为G,
设P(m,-m2+6m-8),如图2,过点P作PN⊥Oy垂足为N,PG⊥Ox垂足为G,
tan∠PAB=$\frac{PG}{DA}$=$\frac{{m}^{2}-6m+8}{m-2}$=$\frac{(m-4)(m-2)}{m-2}$=m-4,
tan∠OPC=$\frac{PN}{CN}$=$\frac{m}{-+6m-8-(-8)}$=$\frac{m}{-m+6m}$=$\frac{1}{6-m}$,
∵∠PAB=∠OCP,
∴$\frac{1}{6-m}$=m-4,即m2-10m+25=0,
∴m=5,
∴P(5,-3)
∴AG=5-2=3,
∴△PAG为等腰直角三角形.
过点B作BH⊥AP,则BH=$\sqrt{2}$,AH=$\sqrt{2}$,AP=3$\sqrt{2}$,
∴PH=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
∴tan∠APB=$\frac{BH}{PH}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$,
∴tan∠APB的值为$\frac{1}{2}$.
点评 本题考查的是二次函数综合题,涉及到锐角三角函数的定义、等腰直角三角形的判定与性质等知识,难度较大,在解答此题时要注意辅助线的做法,先构造出直角三角形,再利用锐角三角函数的定义解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元) | … | 70 | 90 | … |
| 销售量y(件) | … | 300 | 100 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com