
【题目】如图,在△ABC中,CA=CB,∠ABC=72°,BD是高线,BE是角平分线,若AB=12cm,则CE=_______cm,则∠DBE=_____度.

科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的棋子按一定的规律组成,其中第![]() 个图形有
个图形有![]() 颗棋子,第
颗棋子,第![]() 个图形一共有
个图形一共有![]() 颗棋子,第
颗棋子,第![]() 个图形一共有
个图形一共有![]() 颗棋子,,则第
颗棋子,,则第![]() 个图形中棋子的颗数为( )
个图形中棋子的颗数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张三角形纸片ABC,∠A=80°,∠B=70°,D是AC边上一定点,过点D将纸片的一角折叠,使点C落在BC下方C′处,折痕DE与BC交于点E,当AB与∠C′的一边平行时,∠DEC'=_____度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子,出现6的概率是![]() 的意思是每6次就有1次掷得6
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖。
D. 在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51。
查看答案和解析>>
科目:初中数学 来源: 题型:
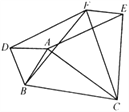
【题目】如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com