
【题目】如图,直角三角形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 绕
绕![]() 点旋转
点旋转![]() 得到
得到![]() .一动点
.一动点![]() 从
从![]() 出发,以每秒1的速度沿
出发,以每秒1的速度沿![]() 的路线匀速运动,过点
的路线匀速运动,过点![]() 作直线
作直线![]() ,使
,使![]() .
.

(1)当点![]() 运动2秒时,另一动点
运动2秒时,另一动点![]() 也从
也从![]() 出发沿
出发沿![]() 的路线运动,且在
的路线运动,且在![]() 上以每秒1的速度匀速运动,在
上以每秒1的速度匀速运动,在![]() 上以每秒2的速度匀速运动,过
上以每秒2的速度匀速运动,过![]() 作直线
作直线![]() 使
使![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 直线
直线![]() 与
与![]() 截四边形
截四边形![]() 所得图形的面积为
所得图形的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
(2)当点![]() 开始运动的同时,另一动点
开始运动的同时,另一动点![]() 从
从![]() 处出发沿
处出发沿![]() 的路线运动,且在
的路线运动,且在![]() 上以每秒
上以每秒![]() 的速度匀速运动,在
的速度匀速运动,在![]() 上以每秒2的速度匀度运动,是否存在这样的
上以每秒2的速度匀度运动,是否存在这样的![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 运动的时间
运动的时间![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
【答案】(1)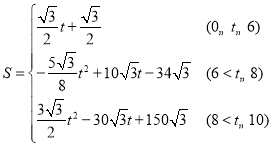 ,S的最大值为
,S的最大值为![]() ;(2)存在,m的值为
;(2)存在,m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分![]() 、
、![]() 和
和![]() 三种情况分别表示出有关线段求得两个变量之间的函数关系即可.
三种情况分别表示出有关线段求得两个变量之间的函数关系即可.
(2)分两种情形:①如图![]() 中,由题意点
中,由题意点![]() 在
在![]() 上运动的时间与点
上运动的时间与点![]() 在
在![]() 上运动的时间相等,即
上运动的时间相等,即![]() .当
.当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别构建方程求解即可.②如图
时,分别构建方程求解即可.②如图![]() 中,作
中,作![]() 于
于![]() .首先证明
.首先证明![]() ,根据
,根据![]() 构建方程即可解决问题.
构建方程即可解决问题.
解:(1)如图![]() 中,当
中,当![]() 时,点
时,点![]() 与点
与点![]() 都在
都在![]() 上运动,
上运动,
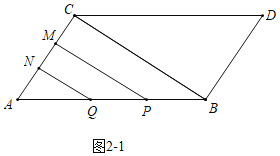
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 此时两平行线截平行四边形
此时两平行线截平行四边形![]() 的面积为
的面积为![]() .
.
如图![]() 中,当
中,当![]() 时,点
时,点![]() 在
在![]() 上运动,点
上运动,点![]() 仍在
仍在![]() 上运动.
上运动.
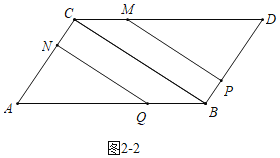
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而![]() ,
,
故此时两平行线截平行四边形![]() 的面积为:
的面积为:
![]()
![]()
![]() ,
,
如图![]() 中,当
中,当![]() 时,点
时,点![]() 和点
和点![]() 都在
都在![]() 上运动.
上运动.
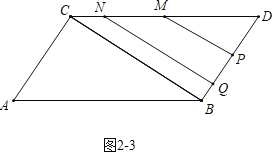
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 此时两平行线截平行四边形
此时两平行线截平行四边形![]() 的面积为
的面积为![]() .
.
故![]() 关于
关于![]() 的函数关系式为
的函数关系式为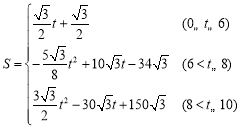 ,
,
当![]() 时,S随t增大而增大,
时,S随t增大而增大,
当![]() 时,S随t增大而增大,
时,S随t增大而增大,
当![]() 时,S随t增大而减小,
时,S随t增大而减小,
∴当t=8时,S最大,代入可得S=![]() ;
;
(2)如图![]() 中,
中,
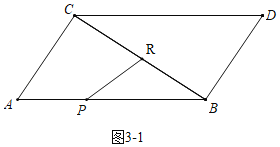
由题意点![]() 在
在![]() 上运动的时间与点
上运动的时间与点![]() 在
在![]() 上运动的时间相等,
上运动的时间相等,![]() .
.
当![]() 时,
时,![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
当![]() 时,则有
时,则有![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,则有
,则有![]() ,解得
,解得![]() .
.
如图![]() 中,作
中,作![]() 于
于![]() .
.
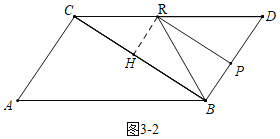
在Rt△CHR中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
当![]() 时,则有
时,则有![]() ,解得
,解得![]() ,
,
综上所述,满足条件的m的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某段地铁工程由甲、乙两工程队合作![]() 天可完成.若单独施工,甲工程队比乙工程队多用
天可完成.若单独施工,甲工程队比乙工程队多用![]() 天.
天.
![]() 求甲、乙两工程队单独完成此项工程各需要多少天?
求甲、乙两工程队单独完成此项工程各需要多少天?
![]() 如果甲工程队施工每天需付施工费
如果甲工程队施工每天需付施工费![]() 万元,乙工程队施工每天需付施工费
万元,乙工程队施工每天需付施工费![]() 万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过
万元,甲工程队最多要单独施工多少天后,再由甲.乙两工程队合作施工完成剩下的工程,才能使施工费不超过![]() 万元?
万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
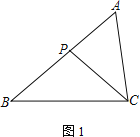
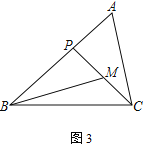
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一驴友分三次从![]() 地出发沿着不同线路(
地出发沿着不同线路(![]() 线、
线、![]() 线、
线、![]() 线)去
线)去![]() 地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;
地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;![]() 线、
线、![]() 线路程相等,都比
线路程相等,都比![]() 线路程多
线路程多![]() ;
;![]() 线总时间等于
线总时间等于![]() 线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完
线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完![]() 线;在
线;在![]() 线中穿越丛林、涉水行走和攀登所用时间分别比
线中穿越丛林、涉水行走和攀登所用时间分别比![]() 线上升了
线上升了![]() .若他用了
.若他用了![]() 小时穿越丛林、
小时穿越丛林、![]() 小时涉水行走和
小时涉水行走和![]() 小时攀登走完
小时攀登走完![]() 线,且
线,且![]() 都为正整数,则
都为正整数,则![]() _____.
_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
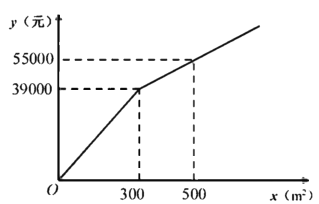
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人一起步行到火车站,途中发现忘带火车票了,于是甲立刻原速返回,乙继续以原速步行前往火车站,甲取完火车票后乘出租车赶往火车站,途中与乙相遇,带上乙一同前往,结果比预计早到3分钟,他们与公司的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图所示,则下列结论错误的是( )
(分)的函数关系如图所示,则下列结论错误的是( )
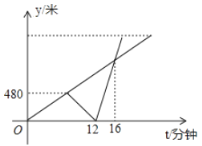
A.他们步行的速度为每分钟80米;B.出租车的速度为每分320米;
C.公司与火车站的距离为1600米;D.出租车与乙相遇时距车站400米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com