
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健康的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽取了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
![]() 本次接受调查的总人数为_____人.
本次接受调查的总人数为_____人.
![]() 请补全条形统计图.
请补全条形统计图.
![]() 该校九年级共有学生
该校九年级共有学生![]() 人,请估计该校九年级学生每天吃早餐的人数;
人,请估计该校九年级学生每天吃早餐的人数;
![]() 请根据此次调查的结果提一条建议.
请根据此次调查的结果提一条建议.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为CD的中点,F为BC边上一点,且EF⊥AE,AF的延长线与DC的延长线交于点G,连接BE,与AF交于点H,则下列结论中不正确的是( )
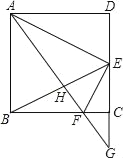
A. AF=CF+BCB. AE平分∠DAF
C. tan∠CGF=![]() D. BE⊥AG
D. BE⊥AG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果进价为每千克15元,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克.设销售单价为![]() (元),每天的销售量为
(元),每天的销售量为![]() (千克),每天获利为
(千克),每天获利为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种水果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )

A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1)
C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
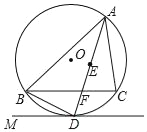
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC;
(1)求证:直线DM是⊙O的切线;
(2)若DF=2,AF=5,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
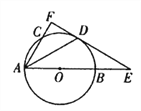
(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①;cos(α+β)=cosαcosβ﹣sinαsinβ②;tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,
如:tan105°=tan(45°+60°)=![]() =
=![]() =
=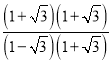 =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
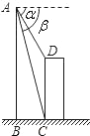
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com