
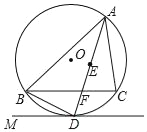
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC;
(1)求证:直线DM是⊙O的切线;
(2)若DF=2,AF=5,求BD长.
【答案】(1)见解析;(2)DB=![]() .
.
【解析】
(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;
(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DFDA,据此解答即可.
(1)如图所示,连接OD,
∵点E是△ABC的内心,

∴∠BAD=∠CAD,
∴![]() ,
,
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
又∵OD为⊙O半径,
∴直线DM是⊙O的切线;
(2)![]() ,
,
∴∠DBF=∠DAB,
又∵∠BDF=∠ADB(公共角),
∴△DBF∽△DAB,
∴![]() =
=![]() ,即DB2=DFDA,
,即DB2=DFDA,
∵DF=2,AF=5∴DA=DF+AF=7
∴DB2=DFDA=14
∴DB=![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
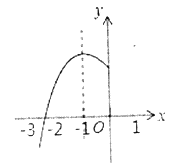
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健康的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽取了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
![]() 本次接受调查的总人数为_____人.
本次接受调查的总人数为_____人.
![]() 请补全条形统计图.
请补全条形统计图.
![]() 该校九年级共有学生
该校九年级共有学生![]() 人,请估计该校九年级学生每天吃早餐的人数;
人,请估计该校九年级学生每天吃早餐的人数;
![]() 请根据此次调查的结果提一条建议.
请根据此次调查的结果提一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
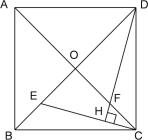
【题目】已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
查看答案和解析>>
科目:初中数学 来源: 题型:
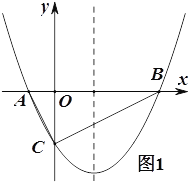
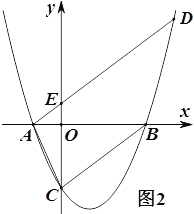
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
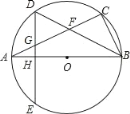
【题目】如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.
①求证:AG=GD;
②当∠ABC满足什么条件时,△DFG是等边三角形?
③若AB=10,sin∠ABD=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com