
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当四边形MENF是正方形时,求AD:AB的值.

【答案】(1)证明见解析(2)菱形(3)2
【解析】
(1)根据矩形的性质得到AB=CD,∠A=∠D=90°,利用SAS定理证明△ABM≌△DCM;
(2)证明ME=MF,根据邻边相等的平行四边形是菱形证明;
(3)证明Rt△BEN≌Rt△CFN,得到∠ENB=∠FNC=45°,∠ABM=45°,得到AB=AM,计算即可.
(1)∵四边形ABCD是矩形,∴AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM.
在△ABM和△DCM中,∵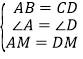 ,∴△ABM≌△DCM;
,∴△ABM≌△DCM;
(2)四边形MENF是菱形.
∵E,F,N分别是BM,CM,CB的中点,∴NE∥MF,NE=MF,∴四边形MENF是平行四边形.
由(1)得:BM=CM,∴ME=MF,∴四边形MENF是菱形;
(3)∵四边形MENF是正方形,∴EN=NF,NE⊥BM,NF⊥MC,
又∵N是BC的中点,∴BN=NC,
在Rt△BEN和Rt△CFN中,
![]() ,∴Rt△BEN≌Rt△CFN,∴∠ENB=∠FNC=45°,∴∠ABM=45°,
,∴Rt△BEN≌Rt△CFN,∴∠ENB=∠FNC=45°,∴∠ABM=45°,
∴AB=AM,
又∵M是AD的中点,∴AD:AB=2.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、 AC于点E、G.连接GF.则下列结论错误的是( )

A. ∠AGD=112.5° B. 四边形AEFG是菱形 C. tan∠AED=2 D. BE=2OG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片ABCD中,AB=2,BC=3,操作:将矩形纸片沿EF折叠,使点B落在边CD上.探究:
(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等给出证明,如果不全等,请说明理由;
(2)如图2,若点B1与CD的中点重合,求△FCB1和△B1DG的周长之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,
(1)点O在线段AB上,以点O为圆心,AO为半径作⊙O,⊙O经过点C。
(要求尺规作图,保留作图痕迹,写结论,不必写作法。)
(2)若∠A=25°,∠B=40°,请判断BC与⊙O的位置关系并写出证明过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,若△PCD中有一个角等于50°,则∠A度数等于__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 点坐标为
点坐标为![]() ,点
,点![]() 从点
从点![]() 出发以1个单位长度/秒的速度沿
出发以1个单位长度/秒的速度沿![]() 轴正半轴方向运动,同时,点
轴正半轴方向运动,同时,点![]() 从点
从点![]() 出发以1个单位长度/秒的速度沿
出发以1个单位长度/秒的速度沿![]() 轴负半轴方向运动,设点
轴负半轴方向运动,设点![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒.以
秒.以![]() 为斜边,向第一象限内作等腰
为斜边,向第一象限内作等腰![]() ,连接
,连接![]() .下列四个说法:
.下列四个说法:
①![]() ;②
;②![]() 点坐标为
点坐标为![]() ;③四边形
;③四边形![]() 的面积为16;④
的面积为16;④![]() .其中正确的说法个数有( )
.其中正确的说法个数有( )

A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com