
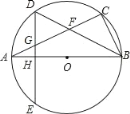
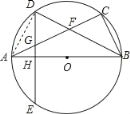
【题目】如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.
①求证:AG=GD;
②当∠ABC满足什么条件时,△DFG是等边三角形?
③若AB=10,sin∠ABD=![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)当∠ABC=60°时,△DFG是等边三角形.理由见解析;(3)BC的长为![]() .
.
【解析】
(1)首先连接AD,由DE⊥AB,AB是![]() 的直径,根据垂径定理,即可得到
的直径,根据垂径定理,即可得到![]() ,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE=∠ABD,又由弦BD平分∠ABC,可得∠DBC=∠ABD,根据等角对等边的性质,即可证得AG=GD;
,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE=∠ABD,又由弦BD平分∠ABC,可得∠DBC=∠ABD,根据等角对等边的性质,即可证得AG=GD;
(2)当∠ABC=60°时,△DFG是等边三角形,根据半圆(或直径)所对的圆周角是直角与三角形的外角的性质,易求得∠DGF=∠DFG=60°,即可证得结论;
(3)利用三角函数先求出tan∠ABD![]() ,cos∠ABD=
,cos∠ABD=![]() ,再求出DF、BF,然后即可求出BC.
,再求出DF、BF,然后即可求出BC.
(1)证明:连接AD,
∵DE⊥AB,AB是⊙O的直径,
∴![]() ,
,
∴∠ADE=∠ABD,
∵弦BD平分∠ABC,
∴∠DBC=∠ABD,
∵∠DBC=∠DAC,
∴∠ADE=∠DAC,
∴AG=GD;
(2)解:当∠ABC=60°时,△DFG是等边三角形.
理由:∵弦BD平分∠ABC,
∴∠DBC=∠ABD=30°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°﹣∠ABC=30°,
∴∠DFG=∠FAB+∠DBA=60°,
∵DE⊥AB,
∴∠DGF=∠AGH=90°﹣∠CAB=60°,
∴△DGF是等边三角形;
(3)解:∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵∠DAC=∠DBC=∠ABD,
∵AB=10,sin∠ABD=![]() ,
,
∴在Rt△ABD中,AD=ABsin∠ABD=6,
∴BD=![]() =8,
=8,
∴tan∠ABD=![]() ,cos∠ABD=
,cos∠ABD=![]() ,
,
在Rt△ADF中,DF=ADtan∠DAF=ADtan∠ABD=6×![]() =
=![]() ,
,
∴BF=BD﹣DF=8﹣![]() =
=![]() ,
,
∴在Rt△BCF中,BC=BFcos∠DBC=BFcos∠ABD=![]() ×
×![]() =
=![]() .
.
∴BC的长为:![]() .
.


科目:初中数学 来源: 题型:
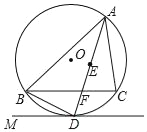
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC;
(1)求证:直线DM是⊙O的切线;
(2)若DF=2,AF=5,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①;cos(α+β)=cosαcosβ﹣sinαsinβ②;tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,
如:tan105°=tan(45°+60°)=![]() =
=![]() =
=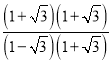 =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
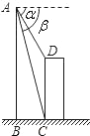
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象经过点A(1,a),B(3,a),且顶点的纵坐标为-4.
的图象经过点A(1,a),B(3,a),且顶点的纵坐标为-4.
(1)求m,n和a的值;
(2)记二次函数图象在点A,B间的部分为G (含点A和点B),若直线![]() 与图象G有公共点,结合函数图象,求k的取值范围.
与图象G有公共点,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
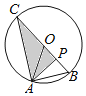
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com