
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
【答案】B
【解析】
分三种情况讨论:①当P在线段OB上,不含端点时;②当点P与点B重合时;③当P与O重合时.分别画出图形,计算即可.
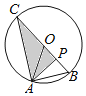
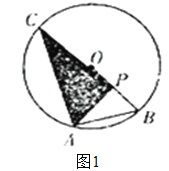
分三种情况讨论:①当P在线段OB上,不含端点时,如图1.
∵△OAB是等边三角形,OB为半径,PC⊥AP,∴C为直线OB与⊙O的另一个交点,∴CB为⊙O的直径,∴CB=6.
∵OA=AB,AP⊥OB,∴OP=PB=![]() OB=1.5,∴CP=CO+OP=3+1.5=4.5.
OB=1.5,∴CP=CO+OP=3+1.5=4.5.
∵∠ACP=30°,∴PC=![]() AP,∴AP=
AP,∴AP=![]() .
.
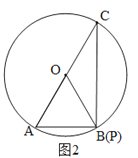
②当点P与点B重合时,如图2,则∠APC=∠ABC=90°,∴AC为直径.
∵∠ACP=30°,∴∠AOB=60°,符合已知条件,∴AP=AB=3.
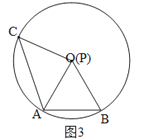
③当P与O重合时,如图3.
∵AP⊥CP,∴∠CPA=∠COA=90°.
∵CO=AO=CP=AP,∴△APC是等腰直角三角形,∴∠ACP=45°,与已知∠ACP=30°矛盾,∴这种情况不成立.
综上所述:AP=3或![]() .
.
故选B.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点![]() 的横坐标,第二个数作为点
的横坐标,第二个数作为点![]() 的纵坐标,则点
的纵坐标,则点![]() 在反比例函数
在反比例函数![]() 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数![]() 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点![]() 的情形;
的情形;
(2)分别求出点![]() 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
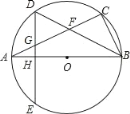
【题目】如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.
①求证:AG=GD;
②当∠ABC满足什么条件时,△DFG是等边三角形?
③若AB=10,sin∠ABD=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
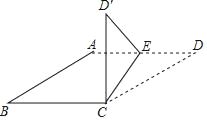
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间甲乙两商场搞促销活动.甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“![]() 元”、“
元”、“![]() 元”、“
元”、“![]() 元”、“
元”、“![]() 元”,顾客每消费满
元”,顾客每消费满![]() 元,就可从箱子里不放回地摸出
元,就可从箱子里不放回地摸出![]() 个球,根据两个小球所标金额之和可获相应价格的礼品.乙商场的方案是:在一个不透明的箱子里放
个球,根据两个小球所标金额之和可获相应价格的礼品.乙商场的方案是:在一个不透明的箱子里放![]() 个完全相同的小球,球上分别标“
个完全相同的小球,球上分别标“![]() 元”、“
元”、“![]() 元”,顾客每消费满
元”,顾客每消费满![]() 元,就可从箱子里不放回地摸出
元,就可从箱子里不放回地摸出![]() 个球,根据两个小球所标金额之和可获相应价格的礼品. 某顾客准备消费
个球,根据两个小球所标金额之和可获相应价格的礼品. 某顾客准备消费![]() 元,
元,
(1)若该顾客在甲商场消费,至少可得价值_________元的礼品,至多可得价值_________元的礼品;
(2)请用画树状图或列表法,说明该顾客去哪个商场消费,获得礼品的总价值不低于![]() 元的概率大.
元的概率大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,3件礼物从外盒包装看完全相同,里面的东西只有颜色不同,将3件礼物放在一起.
(1)甲从中随机抽取一件,求甲抽到不是自己带来的礼物的概率;
(2)每人从中随机抽取一件,求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④![]() ≥2.
≥2.
其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
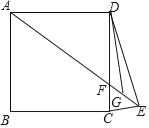
【题目】如图,点E在正方形ABCD的外部,∠DCE=∠DEC,连接AE交CD于点F,∠CDE的平分线交EF于点G,AE=2DG.若BC=8,则AF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com