
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 是
是![]() 的两条弦,过点
的两条弦,过点![]() 作
作![]() ,
,![]() 交
交![]() 的延长线与点
的延长线与点![]() .
.
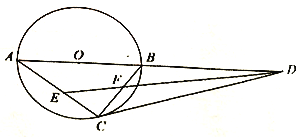
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 与
与![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接OC,由∠A=∠1=∠2且∠2+∠OCB=90°知∠1+∠OCB=90°,据此即可得证;
(2)先△ADC∽△CDB得![]() ,且CD2=ADBD,设CD=4x,CA=4k,知AB=5k,从而得出(4x)2=3x(3x+5k),解关于x的方程,进而得出答案;
,且CD2=ADBD,设CD=4x,CA=4k,知AB=5k,从而得出(4x)2=3x(3x+5k),解关于x的方程,进而得出答案;
(3)由(2)得AB=7、BD=9、CD=12,证DE是∠ADC的平分线知![]() ,求出AC=
,求出AC=![]() ,EC=
,EC=![]() 证得∠A+∠EDA=∠DEC=45°,作DH⊥AC,知△CDH为等腰直角三角形,由BC∥DH知∠CDH=∠1,据此得tan∠CDH=
证得∠A+∠EDA=∠DEC=45°,作DH⊥AC,知△CDH为等腰直角三角形,由BC∥DH知∠CDH=∠1,据此得tan∠CDH=![]() =
=![]() ,继而得DH=CD
,继而得DH=CD![]() =
=![]() ,由DE=
,由DE=![]() 即可解答.
即可解答.
解:(1)如图:
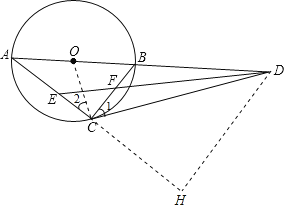
∵OA=OC,
∴∠A=∠2,
∵∠A=∠1,
∴∠1=∠2,
∵AB是⊙O的直径,
∴∠ACB=90°,即∠2+∠OCB=90°,
∴∠1+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线;
(2)![]() ,
,![]()
∴![]() ,又∵
,又∵![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,
,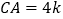
则![]() ,则
,则![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]()
(3)由(2)知AB=5k=7知k=![]() ,则BD=9,CD=4x=4×
,则BD=9,CD=4x=4×![]() k=4×
k=4×![]() ×
×![]() =12,
=12,
∵∠CED=∠A+∠EDC=∠A+∠ADE,
∴∠EDC=∠ADE,即DE是∠ADC的平分线,
∴![]() ,
,
则![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
且![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]()


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象经过点A(1,a),B(3,a),且顶点的纵坐标为-4.
的图象经过点A(1,a),B(3,a),且顶点的纵坐标为-4.
(1)求m,n和a的值;
(2)记二次函数图象在点A,B间的部分为G (含点A和点B),若直线![]() 与图象G有公共点,结合函数图象,求k的取值范围.
与图象G有公共点,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为3的⊙O经过等边△ABO的顶点A、B,点P为半径OB上的动点,连接AP,过点P作PC⊥AP交⊙O于点C,当∠ACP=30°时,AP的长为( )
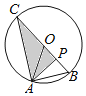
A. 3B. 3或![]() C.
C. ![]() D. 3或
D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线经过![]() ,
,![]() 两点.将
两点.将![]() 绕点
绕点![]() 逆时针旋转90°得到
逆时针旋转90°得到![]() ,点
,点![]() 在抛物线上.
在抛物线上.
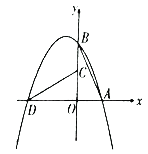
(1)求该抛物线的表达式;
(2)已知点![]() 在
在![]() 轴上(点
轴上(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,若
,若![]() 与
与![]() 相似,试求点
相似,试求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
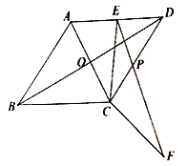
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
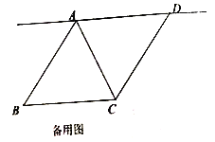
【题目】如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
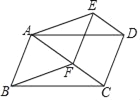
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com