
【题目】如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
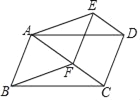
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平行四边形的性质和全等三角形的判定证明即可;
(2)根据平行四边形的判定和菱形的判定解答即可.
(1)∵平行四边形ABCD,∴AD=BC,AD∥BC,∴∠DAC=∠BCF.
∵DE∥AC,∴∠DAC=∠EDA,∴∠FCB=∠EDA.
在△ADE与△BCF中,∵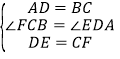 ,∴△ADE≌△BCF(SAS);
,∴△ADE≌△BCF(SAS);
(2)∵DE∥AC,且DE=AC,∴四边形EFCD是平行四边形,∴DC=EF,且DC∥EF.
又∵AB=CD,AB∥CD,∴AB=EF,AB∥EF,∴四边形ABFE是平行四边形.
∵△ADE≌△BCF,∴∠AED=∠BFC.
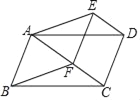
∵∠BAF+∠AED=180°,∴∠BAF+∠BFC=180°.
又∵∠BFA+∠BFC=180°,∴∠BAF=∠BFA,∴BA=BF,∴四边形ABFE为菱形.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=﹣x2+2x.
(1)补全表格:
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
y=﹣x2+2x | (1,1) |
|
| (0,0) |
(2)将抛物线C1向上平移3个单位得到抛物线C2,请画出抛物线C1,C2,并直接回答:抛物线C2与x轴的两交点之间的距离是抛物线C1与x轴的两交点之间距离的多少倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC =10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
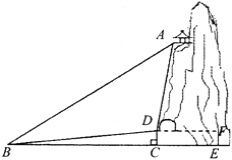
(1)求∠ADB的度数:
(2)过D点作AB的垂线,垂足为G,求DG的长及索道AB的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=2cm,对角线AC、BD交于点O,点E以一定的速度从A向B移动,点F以相同的速度从B向C移动,连结OE、OF、EF.则线段EF的最小值是_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为举办毕业联欢会,小颖设计了一个游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘上的指针所指字母都相同时,他就获得一次指定一位到会者为大家表演节目的机会。(10分)
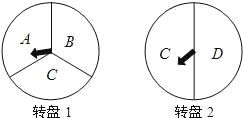
(1)利用树形图或列表的方法表示出游戏可能出现的所有结果。
(2)若小明参加一次游戏,则他能获得这种指定机会的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com