
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
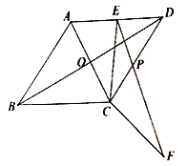
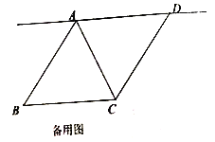
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 14.
14.
【解析】
(1)由菱形的性质得出AD=AB=BC=CD=5,AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD,由勾股定理求出OB,即可得出BD的长;
,OB=OD,由勾股定理求出OB,即可得出BD的长;
(2)①过点C作CH⊥AD于H,由菱形的性质和三角函数得出![]() ,求出AH=2,由勾股定理求出CH=4,求出HE=AE-AH=
,求出AH=2,由勾股定理求出CH=4,求出HE=AE-AH=![]() ,再由勾股定理求出EC,证明△BCD∽△ECF,得出
,再由勾股定理求出EC,证明△BCD∽△ECF,得出![]() ,即可得出结果;
,即可得出结果;
②先证明△BCE≌△DCF,得出BE=DF,当BE最小时,DF就最小,且BE⊥DE时,BE最小,此时∠EBC=∠FDC=90°,BE=DF=4,△EBC的面积=△ABC的面积=△DCF的面积,则四边形ACFD的面积=2△ABC的面积=20,过点F作FH⊥AD于H,过点C作CP⊥AD于P,则∠CPD=90°,证明△PCD∽△HDF,得出![]() ,求出HF=
,求出HF=![]() ,S△ADF=
,S△ADF=![]() ADFH=6,即可得出△ACF的面积.
ADFH=6,即可得出△ACF的面积.
解:(1)∵四边形ABCD是菱形,
∴AD=AB=BC=CD=5,AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD,
,OB=OD,
在Rt△ABO中,由勾股定理得:OB=![]() =
=![]() =2
=2![]() ,
,
∴BD=2OB=4![]() ;
;
(2)①过点C作CH⊥AD于H,如图1所示:
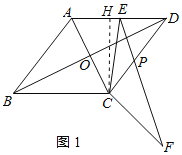
∵四边形ABCD是菱形,
∴∠BAC=∠DAC,
∴cos∠BAC=cos∠DAC,
∴![]() ,即
,即![]() ,
,
∴AH=2,
∴CH=![]() =
=![]() = 4,
= 4,
∵E为AD的中点,
∴AE=![]() AD=
AD=![]() ,
,
∴HE=AE-AH=![]() ,
,
在Rt△CHE中,由勾股定理得:EC=![]() =
=![]() =
=![]() ,
,
由旋转的性质得:∠ECF=∠BCD,CF=CE,
∴![]() ,
,
∴△BCD∽△ECF,
∴![]() ,即
,即![]()
解得:EF=2![]() ;
;
②如图2所示:
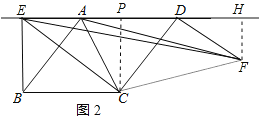
∵∠BCD=∠ECF,
∴∠BCD-DCE=∠ECF-∠DCE,即∠BCE=∠DCF,
在△BCE和△DCF中,
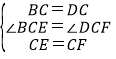 ,
,
∴△BCE≌△DCF(SAS),
∴BE=DF,
当BE最小时,DF就最小,且BE⊥DE时,BE最小,
此时∠EBC=∠FDC=90°,BE=DF=4,△EBC的面积=△ABC的面积=△DCF的面积,则四边形ACFD的面积=2△ABC的面积=5×4=20,
过点F作FH⊥AD于H,过点C作CP⊥AD于P,
则∠CPD=90°,
∴∠PCD+∠PDC=90°,
∵∠FDC=90°,
∴∠PDC+∠HDF=90°,
∴∠PCD=∠HDF,
∴△PCD∽△HDF,
∴![]() ,
,
∴HF=4×![]() =
=![]() ,
,
∴S△ADF=![]() ADHF=
ADHF=![]() ×5×
×5×![]() =6,
=6,
∴S△ACF=S四边形ACFD-S△ADF=20-6=14,
即当DF的长度最小时,△ACF的面积为14.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
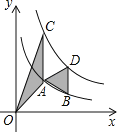
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
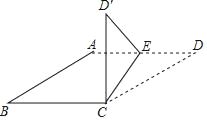
【题目】如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,3件礼物从外盒包装看完全相同,里面的东西只有颜色不同,将3件礼物放在一起.
(1)甲从中随机抽取一件,求甲抽到不是自己带来的礼物的概率;
(2)每人从中随机抽取一件,求甲、乙、丙3人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a≤b)与x轴最多有一个交点.以下四个结论:
①abc>0;
②该抛物线的对称轴在x=﹣1的右侧;
③关于x的方程ax2+bx+c+1=0无实数根;
④![]() ≥2.
≥2.
其中,正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
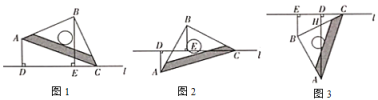
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
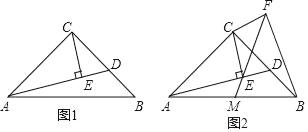
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com