
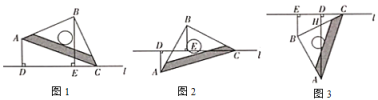
【题目】综合与实践:
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
【答案】(1)①![]() . 理由见解析;②
. 理由见解析;②![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() 的长度为
的长度为![]() .
.
【解析】
(1)过点![]() 作
作![]() 根据已知条件结合直角三角形性质证明
根据已知条件结合直角三角形性质证明![]() ,从而得到四边形
,从而得到四边形![]() 为正方形,最后得出①
为正方形,最后得出①![]() ,直接写出②
,直接写出②![]() (2)过点
(2)过点![]() 作
作![]() ,先证明
,先证明![]() 证明四边形
证明四边形![]() 为正方形,根据正方形的性质求解(3)过点
为正方形,根据正方形的性质求解(3)过点![]() 作
作![]() ,证明
,证明![]() ,四边形
,四边形![]() 为正方形,再求解.
为正方形,再求解.
解:(1)①![]() .
.
理由如下:
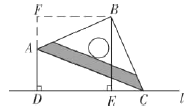
如图,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]()
∴![]()
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
即![]() .
.
在![]() 和
和![]() 中,
中,
∴![]() .
.
∴![]() ,
,![]() .
.
又∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.
∴![]() .
.
∴![]() .
.
②![]() .
.
(2)
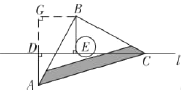
如图,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
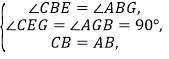
∴![]() .
.
∴![]() ,
,![]() .
.
又∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
(3)
如图,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
同理可证,![]() ,四边形
,四边形![]() 为正方形.
为正方形.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
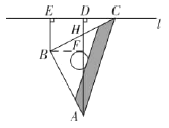
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
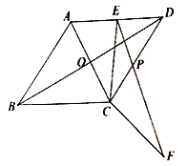
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
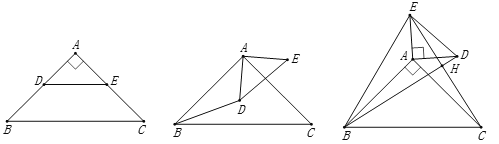
【题目】在数学课堂上,小斐同学和小可同学分别拿着一大一小两个等腰直角三角板,可分别记做![]() 和
和![]() ,其中
,其中![]() .
.
问题的产生:
两位同学先按照如图摆放,点![]() 在
在![]() 上,发现
上,发现![]() 和
和![]() 在数量和位置关系上分别满足
在数量和位置关系上分别满足![]() ,
,![]() .
.
问题的探究:
(1)将![]() 绕点
绕点![]() 逆时针旋转一定角度.如图.点
逆时针旋转一定角度.如图.点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() ,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
,上述结论依然成立吗?如果成立,请证明;如果不成立,请说明理由.
问题的延伸:
继续将![]() 绕点
绕点![]() 逆时针旋转.如图.点
逆时针旋转.如图.点![]() 都在
都在![]() 外部,连结
外部,连结![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.
点.
(2)若![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
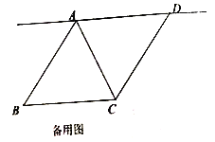
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
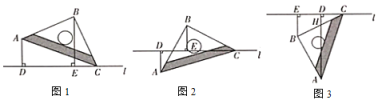
【题目】综合与实践:
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
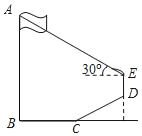
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达到6分及以上为合格,达到9分及以上为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
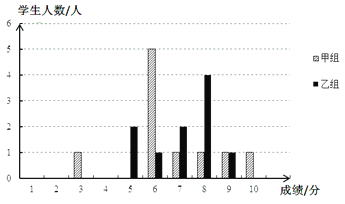
(1)补充完成下列的成绩统计分析表:
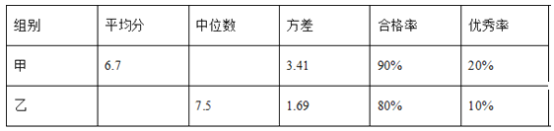
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生;(填“甲”或“乙”)
(3)如果学校准备推荐其中一个组参加区级比赛,你推荐____参加,请你从两个不同的角度说明推荐理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com