
【题目】如图,已知![]() 是矩形
是矩形![]() 内一点,且
内一点,且![]() ,
,![]() ,
,![]() ,那么
,那么![]() 的长为________.
的长为________.
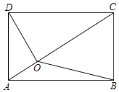
【答案】![]()
【解析】
过O作EF⊥AD于E,交BC于F;过O作GH⊥DC于G,交AB于H,设CF=x,FB=y,AH=s,HB=t,则可得x2-y2=16-9=7,t2-s2=32-12=8,整理得OD2=x2+s2=(y2+t2)-1=9-1=8,即可求得AD的长.
如图,过O作EF⊥AD于E,交BC于F;过O作GH⊥DC于G,交AB于H.
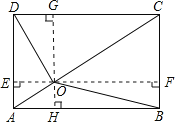
设CF=x,FB=y,AH=s,HB=t,
∴OG=x,DG=s,
∴OF2=OB2-BF2=OC2-CF2,
即42-x2=32-y2,
∴x2-y2=16-9=7①
同理:OH2=12-s2=32-t2
∴t2-s2=32-12=8②
又∵OH2+HB2=OB2,即y2+t2=9;
①-②得(x2+s2)-(y2+t2)=-1,
∴OD2=x2+s2=(y2+t2)-1=9-1=8,
∴OD=2![]() .
.
故答案为:2![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】蜜蜂是自然界神奇的“建筑师“,它能用最少的材料造成最牢固的建筑物“蜂窝“,观察下列的“蜂窝图
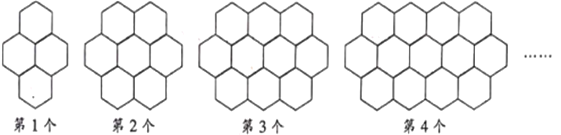
(1)若“![]() ”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
(2)第n个图案中共有多少个建筑单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
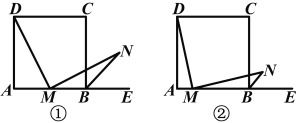
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉二中广雅中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间m分成A、B、C、D四个等级(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
(1)C组的人数是 人,并补全条形统计图.
(2)本次调查的众数是 等,中位数落在 等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
![]()
(1)A、C两点间的距离是多少?
(2)在数轴上找到点D,使点D到B、C两点的距离相等;并在数轴上标出点D表示的数.
(3)若点E与B点的距离是5,求点E表示的数是什么?
(4)若点F与A点的距离是a(a>0),直接写出点F表示的数是多少?(用字母a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E. F.

(1)求证:△OEF是等腰直角三角形。
(2)若AE=4,CF=3,求EF的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com