
【题目】如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
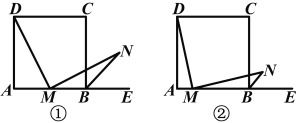
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
【答案】(1)证明:如图①所示,取AD的中点F,连接MF.
∵M是AB的中点,F是AD的中点,
∴![]() ,
,![]() .
.
∵AB=AD,∴AF=AM=DF=MB,
∵∠1=45°,∴∠DFM=135°.
∵BN平分∠CBE,∴∠CBN=45°.
∴∠MBN=135°,∴∠MBN=∠DFM.
∵MN⊥DM,∴△DMN=90°,∴∠NMB+∠DMA=90°.
∵∠A=90°,∴∠ADM+∠DMA=90°.
∴∠NMB=∠ADM.
∴△DFM≌△MBN.∴MD=MN.
(2)MD=MN仍成立.
证明:如图②,在AD上取点F,使AF=AM,连接MF.
由(1)中证法可得DF=BM,∠DFM=∠MBN,∠FDM=∠BMN,
∴△DFM≌△MBN,∴MD=MN.
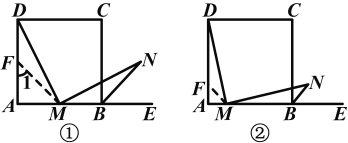
【解析】(1)证MD=MN,可证它们所在的三角形全等,易知MN在钝角△MBN中,而MD在直角△AMD中,显然需添加辅助线构造全等三角形,由△MBN的特征想到可在AD上取AD的中点F,构造△MDF;(2)可参照第(1)题的方法论证.


科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
![]()
(1) 若点A表示数![]() ,当点A向_____ 移动_____个单位长度时,所表示的数恰好是4的相反数.
,当点A向_____ 移动_____个单位长度时,所表示的数恰好是4的相反数.
(2) 若点A表示数![]() ,点B表示数4,当点B不动时,点A向_____移动_____个单位长度或向_____移动_____个单位长度,此时A,B两点间的距离是6.
,点B表示数4,当点B不动时,点A向_____移动_____个单位长度或向_____移动_____个单位长度,此时A,B两点间的距离是6.
(3) 若点A表示数2,将A点向左移动6个单位长度,再向右移动3个单位长度后到达点B,则B表示的数是________,此时 A,B两点间的距离是________.
(4)若A点表示数为a,将A点向右移动b个单位长度,再向左移动c个单位长度后到达点B,则点B表示的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)求上述试验中“2朝下”的频率;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于5的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果10b=n,那么称b为n的劳格数,记为b=d(n).
(1)根据劳格数的定义,可知:d(10)=1,d(102)=2,那么:d(103)= .
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n); d(![]() )=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(
)=d(m)﹣d(n).若d(3)=0.48,d(2)=0.3,根据运算性质,填空:d(6)= ,则d(![]() )= ,d(
)= ,d(![]() )= .
)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,若点
的中点,若点![]() 以
以![]() /秒的速度从点
/秒的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动:点
运动:点![]() 同时以
同时以![]() /秒的速度从点
/秒的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 运动到
运动到![]() 点时停止运动,点
点时停止运动,点![]() 也时停止运动,当点
也时停止运动,当点![]() 运动( )秒时,以点
运动( )秒时,以点![]() 、
、![]() 、
、、
![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
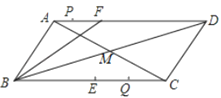
A. 2B. 3C. 3或5D. 4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)试判断△BCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B,C(如图),按要求完成下列问题:
(1)画出直线BC、射线CA、线段AB.
(2)过C点画CD⊥AB,垂足为点D.
(3)在以上的图中,互余的角为 ,互补的角为 .(各写出一对即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com