
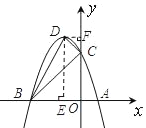
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)试判断△BCD的形状,并说明理由.

【答案】(1)![]() ,D(﹣1,4); (2) △BCD为直角三角形,理由见解析.
,D(﹣1,4); (2) △BCD为直角三角形,理由见解析.
【解析】试题分析:(1)设抛物线的解析式为y=ax2+bx+c,利用待定系数法求得解析式后,通过配方成顶点式,即可得到顶点坐标;
(2)过点D分别作x轴、y轴的垂线,垂足分别为E、F,在Rt△BOC中,由勾股定理可得BC2 =18,在Rt△CDF中,由勾股定理可得CD2 =2,在Rt△BDE中,由勾股定理可得BD2 =20,从而得BC2+CD2=BD2,由勾股定理的逆定理即可得△BCD为直角三角形.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
由抛物线与y轴交于点C(0,3),可知c=3,
即抛物线的解析式为y=ax2+bx+3,
把点A(1,0)、点B(﹣3,0)代入,得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+3,
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D的坐标为(﹣1,4);
(2)△BCD是直角三角形,理由如下:
过点D分别作x轴、y轴的垂线,垂足分别为E、F,
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18,
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
∴CD2=DF2+CF2=2,
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=DE2+BE2=20,
∴BC2+CD2=BD2,
∴△BCD为直角三角形.


科目:初中数学 来源: 题型:
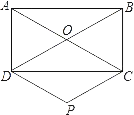
【题目】已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.
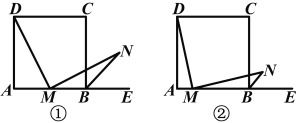
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)﹣23+(﹣3)×|﹣4|﹣(﹣4)2+(﹣2)
(3)3x2﹣(2x2﹣2x)+(4x﹣3x2)
(4)4(a2﹣5a)﹣5(2a2﹣3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
![]()
(1)A、C两点间的距离是多少?
(2)在数轴上找到点D,使点D到B、C两点的距离相等;并在数轴上标出点D表示的数.
(3)若点E与B点的距离是5,求点E表示的数是什么?
(4)若点F与A点的距离是a(a>0),直接写出点F表示的数是多少?(用字母a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了进一步了解八年级学生的身体素质情况,由体育老师随机抽取了八年级 ![]() 名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:


请结合图表完成下列问题:
(1)表中的![]() ,
,![]() ;
;
(2)请把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳的成绩标准是:![]()
![]() 为不合格;
为不合格;![]() 为合格;
为合格;![]() 为良好;
为良好;![]() 为优秀.如果该年级有
为优秀.如果该年级有![]() 名学生,根据以上信息,请你估计该年级跳绳不合格的人数为 ;优秀的人数为 .
名学生,根据以上信息,请你估计该年级跳绳不合格的人数为 ;优秀的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个可以自由转动的均匀转盘A、B,分别被分成4等分和3等分,并在每份内均标有数字.小花为甲、乙两人设计了一个游戏规则如下:同时自由转动转盘A、B;两个转盘停止后,(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),将两个指针所指份内的两个数字相乘,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜.但小强认为这样的规则是不公平的.
(1)请你用一种合适的方法(例如画树状图、列表)帮忙小强说明理由;
(2)请你设计一个公平的规则,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com