
ΓΨΧβΡΩΓΩ[±≥ΨΑ÷Σ Ε] ΐ÷α «≥θ÷– ΐ―ßΒΡ“ΜΗω÷Ί“ΣΙΛΨΏΘ§άϊ”Ο ΐ÷αΩ…“‘ΫΪ ΐ”κ–ΈΆξΟάΒΡΫαΚœΘ°―–ΨΩ ΐ÷αΈ“Ο«ΖΔœ÷ΝΥ–μΕύ÷Ί“ΣΒΡΙφ¬…ΘΚ ΐ÷α…œAΒψΓΔBΒψ±μ ΨΒΡ ΐΈΣaΓΔbΘ§‘ρAΘ§BΝΫΒψ÷°ΦδΒΡΨύάκAB=|a©¹b|Θ§»τaΘΨbΘ§‘ρΩ…ΦρΜ·ΈΣAB=a©¹bΘΜœΏΕΈABΒΡ÷–ΒψM±μ ΨΒΡ ΐΈΣ![]() Θ°
Θ°
[Έ Χβ«ιΨ≥]
“―÷Σ ΐ÷α…œ”–AΓΔBΝΫΒψΘ§Ζ÷±π±μ ΨΒΡ ΐΈΣ©¹10Θ§8Θ§ΒψA“‘ΟΩΟκ3ΗωΒΞΈΜΒΡΥΌΕ»―Ί ΐ÷αœρ”“‘»ΥΌ‘ΥΕ·Θ§ΒψB“‘ΟΩΟκ2ΗωΒΞΈΜœρΉσ‘»ΥΌ‘ΥΕ·Θ°…η‘ΥΕ· ±ΦδΈΣtΟκΘ®tΘΨ0Θ©Θ°
![]()
[ΉέΚœ‘Υ”Ο]
Θ®1Θ©‘ΥΕ·ΩΣ Φ«ΑΘ§AΓΔBΝΫΒψΒΡΨύάκΈΣ ΘΜœΏΕΈABΒΡ÷–ΒψMΥυ±μ ΨΒΡ ΐ Θ°
Θ®2Θ©ΒψA‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐΈΣ ΘΜΒψB‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐΈΣ ΘΜΘ®”ΟΚ§tΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
Θ®3Θ©ΥϋΟ«Α¥…œ ωΖΫ Ϋ‘ΥΕ·Θ§AΓΔBΝΫΒψΨ≠ΙΐΕύ…ΌΟκΜαœύ”ωΘ§œύ”ωΒψΥυ±μ ΨΒΡ ΐ « ≤Ο¥ΘΩ
Θ®4Θ©»τAΘ§BΑ¥…œ ωΖΫ ΫΦΧ–χ‘ΥΕ·œ¬»ΞΘ§œΏΕΈABΒΡ÷–ΒψMΡήΖώ”κ‘≠Βψ÷ΊΚœΘΩ»τΡήΘ§«σ≥ω‘ΥΕ· ±ΦδΘ§≤Δ÷±Ϋ”–¥≥ω÷–ΒψMΒΡ‘ΥΕ·ΖΫœρΚΆ‘ΥΕ·ΥΌΕ»ΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°Θ®Β±AΘ§BΝΫΒψ÷ΊΚœΘ§‘ρ÷–ΒψM“≤”κAΘ§BΝΫΒψ÷ΊΚœΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©18Θ§-1ΘΜΘ®2Θ©©¹10+3tΘ§8©¹2tΘΜΘ®3Θ©AΓΔBΝΫΒψΨ≠Ιΐ![]() ΟκΜαœύ”ωΘ§œύ”ωΒψΥυ±μ ΨΒΡ ΐ «
ΟκΜαœύ”ωΘ§œύ”ωΒψΥυ±μ ΨΒΡ ΐ «![]() ΘΜΘ®4Θ©Ψ≠Ιΐ2ΟκAΘ§BΝΫΒψΒΡ÷–ΒψMΜα”κ‘≠Βψ÷ΊΚœΘ°MΒψΒΡ‘ΥΕ·ΖΫœρœρ”“Θ§‘ΥΕ·ΥΌΕ»ΈΣΟΩΟκ
ΘΜΘ®4Θ©Ψ≠Ιΐ2ΟκAΘ§BΝΫΒψΒΡ÷–ΒψMΜα”κ‘≠Βψ÷ΊΚœΘ°MΒψΒΡ‘ΥΕ·ΖΫœρœρ”“Θ§‘ΥΕ·ΥΌΕ»ΈΣΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ°άμ”…ΦϊΫβΈω
ΗωΒΞΈΜ≥ΛΕ»Θ°άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίAΘ§BΝΫΒψ÷°ΦδΒΡΨύάκAB=|a©¹b|Θ§»τaΘΨbΘ§‘ρΩ…ΦρΜ·ΈΣAB=a©¹bΦΑœΏΕΈABΒΡ÷–ΒψM±μ ΨΒΡ ΐΈΣ![]() Φ¥Ω…«σΫβΘΜ
Φ¥Ω…«σΫβΘΜ
Θ®2Θ©ΒψA‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐ=‘ΥΕ·ΩΣ Φ«ΑAΒψ±μ ΨΒΡ ΐ+ΒψA‘ΥΕ·ΒΡ¬Ζ≥ΧΘ§ΒψB‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐ=‘ΥΕ·ΩΣ Φ«ΑBΒψ±μ ΨΒΡ ΐ©¹ΒψB‘ΥΕ·ΒΡ¬Ζ≥ΧΘΜ
Θ®3Θ©…ηΥϋΟ«Α¥…œ ωΖΫ Ϋ‘ΥΕ·Θ§AΓΔBΝΫΒψΨ≠ΙΐxΟκΜαœύ”ωΘ§Β»ΝΩΙΊœΒΈΣΘΚΒψA‘ΥΕ·ΒΡ¬Ζ≥Χ+ΒψB‘ΥΕ·ΒΡ¬Ζ≥Χ=18Θ§“ά¥ΥΝ–≥ωΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®4Θ©…ηAΘ§BΑ¥…œ ωΖΫ ΫΦΧ–χ‘ΥΕ·tΟκœΏΕΈABΒΡ÷–ΒψMΡήΖώ”κ‘≠Βψ÷ΊΚœΘ§ΗυΨίœΏΕΈABΒΡ÷–Βψ±μ ΨΒΡ ΐΈΣ0Ν–≥ωΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©‘ΥΕ·ΩΣ Φ«ΑΘ§AΓΔBΝΫΒψΒΡΨύάκΈΣ8©¹Θ®©¹10Θ©=18ΘΜœΏΕΈABΒΡ÷–ΒψMΥυ±μ ΨΒΡ ΐΈΣ![]() =©¹1ΘΜ
=©¹1ΘΜ
Θ®2Θ©ΒψA‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐΈΣ©¹10+3tΘΜΒψB‘ΥΕ·tΟκΚσΥυ‘ΎΈΜ÷ΟΒΡΒψ±μ ΨΒΡ ΐΈΣ8©¹2tΘΜ
Θ®3Θ©…ηΥϋΟ«Α¥…œ ωΖΫ Ϋ‘ΥΕ·Θ§AΓΔBΝΫΒψΨ≠ΙΐxΟκΜαœύ”ωΘ§ΗυΨίΧβ“βΒΟ©¹10+3x=8©¹2xΘ§
ΫβΒΟx=![]() Θ§
Θ§
©¹10+3x=![]() Θ°
Θ°
¥πΘΚAΓΔBΝΫΒψΨ≠Ιΐ![]() ΟκΜαœύ”ωΘ§œύ”ωΒψΥυ±μ ΨΒΡ ΐ «
ΟκΜαœύ”ωΘ§œύ”ωΒψΥυ±μ ΨΒΡ ΐ «![]() ΘΜ
ΘΜ
Θ®4Θ©”…Χβ“βΒΟΘ§![]() =0Θ§
=0Θ§
ΫβΒΟt=2Θ§
¥πΘΚΨ≠Ιΐ2ΟκAΘ§BΝΫΒψΒΡ÷–ΒψMΜα”κ‘≠Βψ÷ΊΚœΘ°MΒψΒΡ‘ΥΕ·ΖΫœρœρ”“Θ§‘ΥΕ·ΥΌΕ»ΈΣΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ°
ΗωΒΞΈΜ≥ΛΕ»Θ°
Ι ¥πΑΗΈΣ18Θ§©¹1ΘΜ©¹10+3tΘ§8©¹2tΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
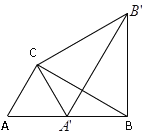
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§ΓœABC=30ΓψΘ§AC=2cmΘ°œ÷‘ΎΫΪΓςABC»ΤΒψCΡφ ±’κ–ΐΉΣ÷ΝΓςAΓδBΓδCΓδΘ§ ΙΒΟΒψAΓδ«ΓΚΟ¬δ‘ΎAB…œΘ§Ν§Ϋ”BBΓδΘ§‘ρBBΓδΒΡ≥ΛΕ»ΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
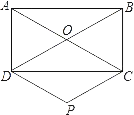
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§Ε‘Ϋ«œΏAC”κBDœύΫΜ”ΎΒψOΘ§ΙΐΒψCΘ§DΖ÷±πΉςBDΘ§ACΒΡΤΫ––œΏΘ§ΝΫœΏœύΫΜ”ΎΒψPΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈCODP «Νβ–ΈΘΜ
Θ®2Θ©Β±ΨΊ–ΈABCDΒΡ±ΏADΘ§DC¬ζΉψ ≤Ο¥ΙΊœΒ ±Θ§Νβ–ΈCODP «’ΐΖΫ–ΈΘΩ«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ ΐ―ßΆΊ’ΙΩΈ…œΘ§άœ Π»ΟΆ§―ßΟ«ΧΫΧ÷ΧΊ βΥΡ±Ώ–ΈΒΡΉωΖ®ΘΚ
»γΆΦΘ§œ»ΉςœΏΕΈ![]() Θ§Ής…δœΏ
Θ§Ής…δœΏ![]() Θ®
Θ®![]() ΈΣ»ώΫ«Θ©Θ§Ιΐ
ΈΣ»ώΫ«Θ©Θ§Ιΐ![]() Ής…δœΏ
Ής…δœΏ![]() ΤΫ––”Ύ
ΤΫ––”Ύ![]() Θ§‘ΌΉς
Θ§‘ΌΉς![]() ΚΆ
ΚΆ![]() ΒΡΤΫΖ÷œΏΖ÷±πΫΜ
ΒΡΤΫΖ÷œΏΖ÷±πΫΜ![]() ΚΆ
ΚΆ![]() ”ΎΒψ
”ΎΒψ![]() ΚΆ
ΚΆ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§‘ρΥΡ±Ώ–Έ
Θ§‘ρΥΡ±Ώ–Έ![]() ΈΣΝβ–ΈΘΜ
ΈΣΝβ–ΈΘΜ
Θ®1Θ©Ρψ»œΈΣΗΟΉςΖ®’ΐ»Ζ¬πΘΩ«κΥΒΟςάμ”….
Θ®2Θ©»τ![]() Θ§≤Δ«“ΥΡ±Ώ–Έ
Θ§≤Δ«“ΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§‘Ύ
Θ§‘Ύ![]() …œ»Γ“ΜΒψ
…œ»Γ“ΜΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() .«κΈ ΆΦ÷–¥φ‘Ύ’β―υΒΡΒψ
.«κΈ ΆΦ÷–¥φ‘Ύ’β―υΒΡΒψ![]() ¬πΘΩ»τ¥φ‘ΎΘ§‘ρ«σ≥ω
¬πΘΩ»τ¥φ‘ΎΘ§‘ρ«σ≥ω![]() ΒΡ≥ΛΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ≥ΛΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®1Θ§1Θ©Θ§BΘ®4Θ§2Θ©Θ§CΘ®3Θ§4Θ©.
(1) «κΜ≠≥ωΓςABCœρΉσΤΫ“Τ5ΗωΒΞΈΜ≥ΛΕ»ΚσΒΟΒΫΒΡΓςA![]() B
B![]() C
C![]() ΘΜ
ΘΜ
(2) «κΜ≠≥ωΓςABCΙΊ”Ύ‘≠ΒψΕ‘≥ΤΒΡΓςA![]() B
B![]() C
C![]() ΘΜ
ΘΜ
(3) ‘Ύ![]() ÷α…œ«σΉς“ΜΒψPΘ§ ΙΓςPABΒΡ÷ή≥ΛΉν–ΓΘ§«κΜ≠≥ωΓςPABΘ§≤Δ÷±Ϋ”–¥≥ωPΒΡΉχ±ξ.
÷α…œ«σΉς“ΜΒψPΘ§ ΙΓςPABΒΡ÷ή≥ΛΉν–ΓΘ§«κΜ≠≥ωΓςPABΘ§≤Δ÷±Ϋ”–¥≥ωPΒΡΉχ±ξ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΤΏΡξΦΕΩΣ’Ι―ίΫ≤±»»ϋΘ§―ß–ΘΨωΕ®ΙΚ¬ρ“Μ–©± Φ«±ΨΚΆΗ÷± ΉςΈΣΫ±ΤΖΘ°œ÷”–ΦΉΓΔ““ΝΫΦ“…ΧΒξ≥ω έΝΫ÷÷Ά§―υΒΡ± Φ«±ΨΚΆΗ÷± Θ°ΥϊΟ«ΒΡΕ®ΦέœύΆ§ΘΚ± Φ«±ΨΕ®ΦέΈΣΟΩ±Ψ25‘ΣΘ§Η÷± ΟΩ÷ßΕ®Φέ6‘ΣΘ§ΒΪ «ΥϊΟ«ΒΡ”≈ΜίΖΫΑΗ≤ΜΆ§Θ§ΦΉΒξΟΩ¬ρ“Μ±Ψ± Φ«±Ψ‘υ“Μ÷ßΗ÷± ΘΜ““Βξ»Ϊ≤ΩΑ¥Ε®ΦέΒΡ9’έ”≈ΜίΘ°“―÷ΣΤΏΡξΦΕ–η± Φ«±Ψ20±ΨΘ§Η÷± x÷ßΘ®¥σ”Ύ20÷ßΘ©Θ°Έ ΘΚ
Θ®1Θ©‘ΎΦΉΒξΙΚ¬ρ–ηΗΕΩνΓΓ ‘ΣΘ§‘Ύ““ΒξΙΚ¬ρ–ηΗΕΩνΓΓ ‘ΣΘΜ
Θ®2Θ©»τx=30Θ§Ά®ΙΐΦΤΥψΥΒΟς¥Υ ±ΒΫΡΡΦ“…ΧΒξΙΚ¬ρΫœΈΣΚœΥψΘΩ
Θ®3Θ©Β±x=40 ±Θ§«κ…ηΦΤ“Μ÷÷ΖΫΑΗΘ§ ΙΙΚ¬ρΉν Γ«°ΘΩΥψ≥ω¥Υ ±–η“ΣΗΕΩνΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΔΌΥυ ΨΘ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§M «ABΒΡ÷–ΒψΘ§E «ABΒΡ―”≥ΛœΏ…œ“ΜΒψΘ§MNΓΆDMΘ§«“ΫΜΓœCBEΒΡΤΫΖ÷œΏ”ΎΒψNΘ°
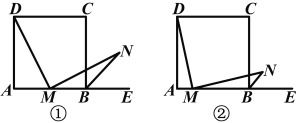
(1)«σ÷ΛΘΚMDΘΫMNΘΜ
(2)»τΫΪ…œ ωΧθΦΰ÷–ΓΑM «ABΒΡ÷–ΒψΓ±ΗΡ≥…ΓΑM «AB…œ»Έ“β“ΜΒψΓ±Θ§Τδ”ύΧθΦΰ≤Μ±δΘ§»γΆΦΔΎΥυ ΨΘ§‘ρΫα¬έΓΑMDΘΫMNΓ±ΜΙ≥…ΝΔ¬πΘΩ»τ≥…ΝΔΘ§Ηχ≥ω÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓœAOBΘΫ90ΓψΘ§‘ΎΓœAOBΒΡΤΫΖ÷œΏOM…œ”–“ΜΒψCΘ§ΫΪ“ΜΗω»ΐΫ«ΑεΒΡ÷±Ϋ«ΕΞΒψ”κC÷ΊΚœΘ§ΥϋΒΡΝΫΧθ÷±Ϋ«±ΏΖ÷±π”κOAΘ§OB(ΜρΥϋΟ«ΒΡΖ¥œρ―”≥ΛœΏ)œύΫΜ”ΎΒψDΘ§E.
Β±»ΐΫ«Αε»ΤΒψC–ΐΉΣΒΫCD”κOA¥Ι÷± ±(»γΆΦΔΌ)Θ§“Ή÷ΛΘΚODΘΪOEΘΫ![]() OCΘΜ
OCΘΜ
Β±»ΐΫ«Αε»ΤΒψC–ΐΉΣΒΫCD”κOA≤Μ¥Ι÷± ±Θ§Φ¥‘ΎΆΦΔΎΘ§ΆΦΔέ’βΝΫ÷÷«ιΩωœ¬Θ§…œ ωΫα¬έ «Ζώ»‘»Μ≥…ΝΔΘΩ»τ≥…ΝΔΘ§«κΗχ”η÷ΛΟςΘΜ»τ≤Μ≥…ΝΔΘ§œΏΕΈODΘ§OEΘ§OC÷°Φδ”÷”–‘θ―υΒΡ ΐΝΩΙΊœΒΘΩ«κ–¥≥ωΡψΒΡ≤¬œκΘ§≤Μ–η÷ΛΟςΘ°
 ΓΓΓΓ
ΓΓΓΓ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΈΣΝΥΫχ“Μ≤ΫΝΥΫβΑΥΡξΦΕ―ß…ζΒΡ…μΧεΥΊ÷ «ιΩωΘ§”…Χε”ΐάœ ΠΥφΜζ≥ι»ΓΝΥΑΥΡξΦΕ ![]() Οϊ―ß…ζΫχ––“ΜΖ÷÷”Χχ…ΰ≤β ‘Θ§“‘≤β ‘ ΐΨίΈΣ―υ±ΨΘ§Μφ÷Τ≥ω≤ΩΖ÷ΤΒ ΐΖ÷≤Φ±μΚΆ≤ΩΖ÷ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ°»γœ¬Υυ ΨΘΚ
Οϊ―ß…ζΫχ––“ΜΖ÷÷”Χχ…ΰ≤β ‘Θ§“‘≤β ‘ ΐΨίΈΣ―υ±ΨΘ§Μφ÷Τ≥ω≤ΩΖ÷ΤΒ ΐΖ÷≤Φ±μΚΆ≤ΩΖ÷ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ°»γœ¬Υυ ΨΘΚ


«κΫαΚœΆΦ±μΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±μ÷–ΒΡ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©«κΑ―ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»τΑΥΡξΦΕ―ß…ζ“ΜΖ÷÷”Χχ…ΰΒΡ≥…Φ®±ξΉΦ «ΘΚ![]()
![]() ΈΣ≤ΜΚœΗώΘΜ
ΈΣ≤ΜΚœΗώΘΜ![]() ΈΣΚœΗώΘΜ
ΈΣΚœΗώΘΜ![]() ΈΣΝΦΚΟΘΜ
ΈΣΝΦΚΟΘΜ![]() ΈΣ”≈–ψΘ°»γΙϊΗΟΡξΦΕ”–
ΈΣ”≈–ψΘ°»γΙϊΗΟΡξΦΕ”–![]() Οϊ―ß…ζΘ§ΗυΨί“‘…œ–≈œΔΘ§«κΡψΙάΦΤΗΟΡξΦΕΧχ…ΰ≤ΜΚœΗώΒΡ»Υ ΐΈΣ ΘΜ”≈–ψΒΡ»Υ ΐΈΣ Θ°
Οϊ―ß…ζΘ§ΗυΨί“‘…œ–≈œΔΘ§«κΡψΙάΦΤΗΟΡξΦΕΧχ…ΰ≤ΜΚœΗώΒΡ»Υ ΐΈΣ ΘΜ”≈–ψΒΡ»Υ ΐΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com