
ЁОЬтФПЁПФГаЃЭХЮЏОйАьСЫвЛДЮЁАжаЙњУЮЃЌЮвЕФУЮЁБбнНВБШШќЃЌТњЗж10ЗжЃЌбЇЩњЕУЗжОљЮЊећЪ§ЃЌГЩМЈДяЕН6ЗжМАвдЩЯЮЊКЯИёЃЌДяЕН9ЗжМАвдЩЯЮЊгХауЃЎетДЮОКШќжаМзЁЂввСНзщбЇЩњГЩМЈЗжВМЕФЬѕаЮЭГМЦЭМШчЯТЃЎ
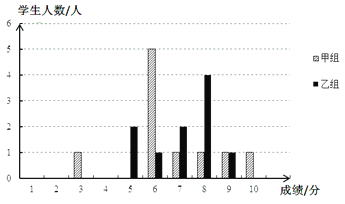
ЃЈ1ЃЉВЙГфЭъГЩЯТСаЕФГЩМЈЭГМЦЗжЮіБэЃК
ЃЈ2ЃЉаЁУїЭЌбЇЫЕЃКЁАетДЮОКШќЮвЕУСЫ7ЗжЃЌдкЮвУЧаЁзщжаХХУћЪєжагЮТдЦЋЩЯЃЁЁБЙлВьЩЯБэПЩжЊЃЌаЁУїЪЧЁЁ зщбЇЩњЃЛЃЈЬюЁАМзЁБЛђЁАввЁБЃЉ
ЃЈ3ЃЉШчЙћбЇаЃзМБИЭЦМіЦфжавЛИізщВЮМгЧјМЖБШШќЃЌФуЭЦМі____ВЮМгЃЌЧыФуДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦМіРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћБэИёЃЛЃЈ2ЃЉМзЃЛЃЈ3ЃЉМзЛђвв.
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнЬѕаЮЭГМЦЭМаДГіМзввСНзщЕФГЩМЈЃЌШЛКѓЗжБ№МЦЫуМзЕФжаЮЛЪ§ЃЌввЕФЦНОљЪ§КЭЗНВюЃЛ
ЃЈ2ЃЉБШНЯСНзщЕФжаЮЛЪ§НјааХаЖЯЃЛ
ЃЈ3ЃЉЭЈЙ§МззщЕФКЯИёТЪЃЌгХауТЪЛђввзщЕФЦНОљЪ§ЁЂжаЮЛЪ§ЛђЗНВюНјааЫЕУїЃЎ
ЃЈ1ЃЉМззщЃК3ЃЌ6ЃЌ6ЃЌ6ЃЌ6ЃЌ6ЃЌ7ЃЌ8ЃЌ9ЃЌ10ЃЌжаЮЛЪ§ЮЊ6ЃЛ
ввзщЃК5ЃЌ5ЃЌ6ЃЌ7ЃЌ7ЃЌ8ЃЌ8ЃЌ8ЃЌ8ЃЌ9ЃЌЦНОљЪ§=7.1ЃЌSвв2=1.69ЃЛ
ЬюБэШчЯТЃК
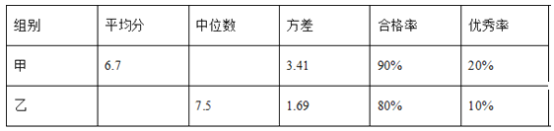
зщБ№ | ЦНОљЗж | жаЮЛЪ§ | ЗНВю | КЯИёТЪ | гХауТЪ |
Мз | 6.7 | 6 | 3.41 | 90% | 20% |
вв | 7.1 | 7.5 | 1.69 | 80% | 10% |
ЃЈ2ЃЉЃЈ2ЃЉвђЮЊМззщЕФжаЮЛЪ§ЮЊ6ЃЌЫљвд7ЗждкМззщХХУћЪєжагЮТдЦЋЩЯЃЛ
ЃЈ3ЃЉМзЛђвв
МззщЃКМззщЕФКЯИёТЪЁЂгХауТЪОљИпгкввзщ.
ЃЈввзщЕФЦНОљЗжЁЂжаЮЛЪ§ОљИпгкМззщЃЌЧвввзщЕФГЩМЈБШМззщЕФГЩМЈЮШЖЈЃЎЃЉ


 ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЪЕМљЃК
ШчЭМ1ЃЌНЋвЛИіЕШбќжБНЧШ§НЧГп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЗХжУдкжБЯп
ЗХжУдкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЙлВьЗЂЯжЃК
ЃЈ1ЃЉШчЭМ1ЃЎЕБ![]() ЃЌ
ЃЌ![]() СНЕуОљдкжБЯп
СНЕуОљдкжБЯп![]() ЕФЩЯЗНЪБЃЌ
ЕФЩЯЗНЪБЃЌ
ЂйВТВтЯпЖЮ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкжБНгаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЛ
ЕФЪ§СПЙиЯЕЃЛ
ВйзїжЄУїЃК
ЃЈ2ЃЉНЋЕШбќжБНЧШ§НЧГп![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыа§зЊжСЭМ2ЮЛжУЪБЃЌЯпЖЮ
ФцЪБеыа§зЊжСЭМ2ЮЛжУЪБЃЌЯпЖЮ![]() ЃЌ
ЃЌ![]() гы
гы![]() гжгадѕбљЕФЪ§СПЙиЯЕЃЌЧыаДГіФуЕФВТЯыЃЌВЂаДГіжЄУїЙ§ГЬЃЛ
гжгадѕбљЕФЪ§СПЙиЯЕЃЌЧыаДГіФуЕФВТЯыЃЌВЂаДГіжЄУїЙ§ГЬЃЛ
ЭиЙуЬНЫїЃК
ЃЈ3ЃЉНЋЕШбќжБНЧШ§гУГп![]() ШЦзХЕу
ШЦзХЕу![]() МЬаја§зЊжСЭМ3ЮЛжУЪБЃЌ
МЬаја§зЊжСЭМ3ЮЛжУЪБЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
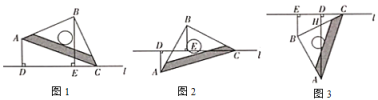
ЁОЬтФПЁПдкЕШбќRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌЕуDЪЧБпBCЩЯШЮвтвЛЕуЃЌСЌНгADЃЌЙ§ЕуCзїCEЁЭADгкЕуEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯBAD=15ЁуЃЌЧвCE=1ЃЌЧѓЯпЖЮBDЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуCзїCFЁЭCEЃЌЧвCF=CEЃЌСЌНгFEВЂбгГЄНЛABгкЕуMЃЌСЌНгBFЃЌЧѓжЄЃКAM=BMЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЮфПе§дкВЮМгШЋЙњЁАЪ§бЇОКШќЁБЃЌжЛвЊЫћдйД№ЖдзюКѓСНЕРЕЅбЁЬтОЭФмЫГРћЙ§ЙиЃЌЦфжаЕквЛЕРЬтга3ИібЁЯюЃЌЕкЖўЕРЬтга4ИібЁЯюЃЌЖјетСНЕРЬтМЮфПЖМВЛЛсЃЌВЛЙ§МЮфПЛЙгавЛДЮЁАЧѓжњЁБУЛгаЪЙгУЃЈЪЙгУЁАЧѓжњЁБПЩШУжїГжШЫШЅЕєЦфжавЛЬтЕФвЛИіДэЮѓбЁЯюЃЉЃЎ
ЃЈ1ЃЉШчЙћМЮфПЕквЛЬтВЛЪЙгУЁАЧѓжњЁБЃЌЫцЛњбЁдёвЛИібЁЯюЃЌФЧУДМЮфПД№ЖдЕквЛЕРЬтЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉШєМЮфПНЋЁАЧѓжњЁБСєдкЕкЖўЬтЪЙгУЃЌЧыгУЛЪїзДЭМЛђСаБэЗЈЧѓМЮфПФмЫГРћЙ§ЙиЕФИХТЪЃЛ
ЃЈ3ЃЉЧыФуДгИХТЪЕФНЧЖШЗжЮіЃЌНЈвщМЮКщдкЕкМИЬтЪЙгУЁАЧѓжњЁБЃЌВХФмЪЙЫћЙ§ЙиЕФИХТЪНЯДѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮжНЦЌABCDЃЌCD=5ЃЌBC=2ЃЌЁЯA=60ЁуЃЌНЋжНЦЌелЕўЃЌЪЙЕуAТфдкЩфЯпADЩЯЃЈМЧЮЊЕуAЁфЃЉЃЌелКлгыABНЛгкЕуPЃЌЩшAPЕФГЄЮЊxЃЌелЕўКѓжНЦЌжиЕўВПЗжЕФУцЛ§ЮЊyЃЌПЩвдБэЪОyгыxжЎМфЙиЯЕЕФДѓжТЭМЯѓЪЧЃЈЁЁЁЁЃЉ
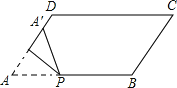
A. 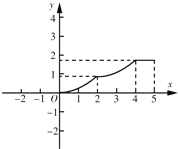 B.
B. 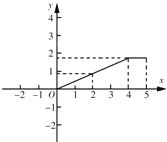
C. 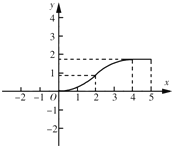 D.
D. 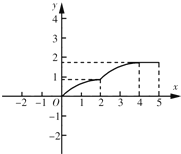
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёФъЮвЪаЮЊДДЦРЁАШЋЙњЮФУїГЧЪаЁБГЦКХЃЌжмФЉЭХЪаЮЏзщжЏжОдИепНјаааћДЋЛюЖЏЃЎАржїШЮДоРЯЪІОіЖЈДг4УћХЎАрИЩВПЃЈаЁдУЁЂаЁЛнЁЂаЁбоКЭаЁйЛЃЉжаЭЈЙ§ГщЧЉЗНЪНШЗЖЈ2УћХЎЩњШЅВЮМгЃЎГщЧЉЙцдђЃКНЋ4УћХЎАрИЩВПаеУћЗжБ№аДдк4еХЭъШЋЯрЭЌЕФПЈЦЌе§УцЃЌАбЫФеХПЈЦЌБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРУцЩЯЃЌДоРЯЪІЯШДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌМЧЯТаеУћЃЌдйДгЪЃгрЕФ3еХПЈЦЌжаЫцЛњГщШЁЕкЖўеХЃЌМЧЯТаеУћЃЎ[ЙцЖЈЃКаЁдУЁЂаЁЛнЁЂаЁбоКЭаЁйЛЕФаеУћЗжБ№МЧзїЃКAЁЂBЁЂCЁЂD]
ЃЈ1ЃЉЁАаЁдУБЛГщжаЁБЪЧ ЪТМўЃЈЬюЁАВЛПЩФмЁБЛђЁАБиШЛЁБЛђЁАЫцЛњЁБЃЉЃЛЕквЛДЮГщШЁПЈЦЌЁАаЁдУБЛГщжаЁБЕФИХТЪЮЊ ЃЛ
ЃЈ2ЃЉЪдгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіЁАаЁЛнБЛГщжаЁБЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=8РхУзЃЌAC=16РхУзЃЌЕуPДгAГіЗЂЃЌвдУПУы2РхУзЕФЫйЖШЯђBдЫЖЏЃЌЕуQДгCЭЌЪБГіЗЂЃЌвдУПУы3РхУзЕФЫйЖШЯђAдЫЖЏЃЌЦфжавЛИіЖЏЕуЕНЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЯргІЭЃжЙдЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊtЃЎ
ЂХгУКЌtЕФДњЪ§ЪНБэЪОЃКAP=ЁЁ ЁЁЃЌAQ=ЁЁ ЁЁЃЎ
ЂЦЕБвдAЃЌPЃЌQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЪБЃЌЧѓдЫЖЏЪБМфЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпLЃКy=Љ![]() x+2гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌдкyжсЩЯгавЛЕуNЃЈ0ЃЌ4ЃЉЃЌЖЏЕуMДгAЕувдУПУы1ИіЕЅЮЛЕФЫйЖШдШЫйбиxжсЯђзѓвЦЖЏЃЎ
x+2гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌдкyжсЩЯгавЛЕуNЃЈ0ЃЌ4ЃЉЃЌЖЏЕуMДгAЕувдУПУы1ИіЕЅЮЛЕФЫйЖШдШЫйбиxжсЯђзѓвЦЖЏЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЃК_____ЃЛЕуBЕФзјБъЃК_____ЃЛ
ЃЈ2ЃЉЧѓЁїNOMЕФУцЛ§SгыMЕФвЦЖЏЪБМфtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкyжсгвБпЃЌЕБtЮЊКЮжЕЪБЃЌЁїNOMЁеЁїAOBЃЌЧѓГіДЫЪБЕуMЕФзјБъЃЛ
ЃЈ4ЃЉдкЃЈ3ЃЉЕФЬѕМўЯТЃЌШєЕуGЪЧЯпЖЮONЩЯвЛЕуЃЌСЌНсMGЃЌЁїMGNбиMGелЕўЃЌЕуNЧЁКУТфдкxжсЩЯЕФЕуHДІЃЌЧѓЕуGЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
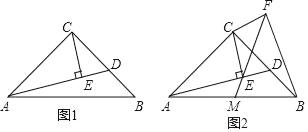
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=![]() x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ
x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЙ§ЕуPЧвгыyжсЦНааЕФжБЯпlгыжБЯпABЁЂACЗжБ№НЛгкЕуEЁЂFЃЌЕБЫФБпаЮAECPЕФУцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуPЮЊХзЮяЯпЕФЖЅЕуЪБЃЌдкжБЯпACЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдCЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com