
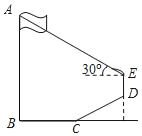
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
【答案】(1)![]() 米(2)(4
米(2)(4![]() +1.5)米
+1.5)米
【解析】
(1)延长ED交射线BC于点H.由题意得DH⊥BC.解直角三角形即可得到结论;
(2)过点E作EF⊥AB于F.得到∠AEF=30°.推出四边形FBHE为矩形.根据矩形的性质得到EF=BH=BC+CH=9.解直角三角形即可得到结论.
(1)延长ED交射线BC于点H.
由题意得:DH⊥BC.
在Rt△CDH中,∠DHC=90°,tan∠DCH=i=1:![]() ,∴∠DCH=30°,∴CD=2DH.
,∴∠DCH=30°,∴CD=2DH.
∵CD=2![]() ,∴DH
,∴DH![]() ,CH=3.
,CH=3.
答:点D的铅垂高度是![]() 米.
米.
(2)过点E作EF⊥AB于F.
由题意得:∠AEF即为点E观察点A时的仰角,∴∠AEF=30°.
∵EF⊥AB,AB⊥BC,ED⊥BC,∴∠BFE=∠B=∠BHE=90°,∴四边形FBHE为矩形,∴EF=BH=BC+CH=9,FB=EH=ED+DH=1.5![]() .
.
在Rt△AEF中,∠AFE=90°,AF=EFtan∠AEF=9![]() ,∴AB=AF+FB=3
,∴AB=AF+FB=3![]() 1.5.
1.5.
答:旗杆AB的高度约为(4![]() 1.5)米.
1.5)米.



 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:

(1)求本次被抽查的学生共有多少名?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“![]() ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;
(4)估计全校“![]() ”等级的学生有多少名?
”等级的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行了“校园好声音”演唱比赛活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.

根据图中提供的信息,回答下列问题:
(1)求参加演唱比赛的学生共有多少人,并把条形图补充完整;
(2)求出扇形统计图中,m= ,n= ;
(3)求出C等级对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
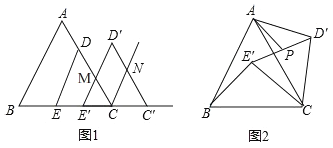
查看答案和解析>>
科目:初中数学 来源: 题型:
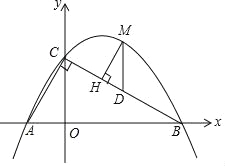
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB为⊙O直径,PQ与⊙O交于点C,AD⊥PQ于点D,且AC为∠DAB的平分线,BE⊥PQ于点E.
(1)求证:PQ与⊙O相切;
(2)求证:点C是DE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为5元,若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份,该店每天固定支出费用为600元![]() 不含套餐成本
不含套餐成本![]() 为了便于结算,每份套餐的售价取整数,设每份套餐的售价为
为了便于结算,每份套餐的售价取整数,设每份套餐的售价为![]() 元,该店日销售利润为y元
元,该店日销售利润为y元![]() 日销售利润
日销售利润![]() 每天的销售额
每天的销售额![]() 套餐成本
套餐成本![]() 每天固定支出
每天固定支出![]()
![]() 求y与x的函数关系式并写出自变量的取值范围.
求y与x的函数关系式并写出自变量的取值范围.
![]() 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在足球场上练习足球传球,足球从一个人传到另一个人记为踢一次.如果从小强开始踢,经过两次踢球后,足球踢到小华处的概率是多少?经过三次踢球后,足球踢回到小强处的概率呢?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上对应的数为20,以原点O为圆心,OA为半径作优弧![]() ,使点B在O右下方,且tan∠AOB=
,使点B在O右下方,且tan∠AOB=![]() ,在优弧
,在优弧![]() 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
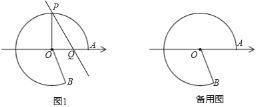
(1)若优弧上一段![]() 的长为10π,求∠AOP度数及x的值.
的长为10π,求∠AOP度数及x的值.
(2)若线段PQ的长为10,求这时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com