
【题目】如图,已知:AB为⊙O直径,PQ与⊙O交于点C,AD⊥PQ于点D,且AC为∠DAB的平分线,BE⊥PQ于点E.
(1)求证:PQ与⊙O相切;
(2)求证:点C是DE的中点.

科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
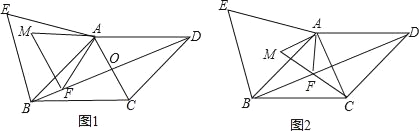
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
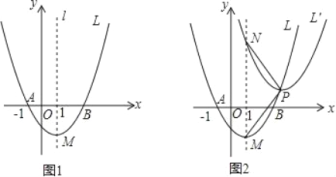
【题目】如图1,已知抛物线L:y=ax2+bx﹣1.5(a>0)与x轴交于点A(-1,0)和点B,顶点为M,对称轴为直线l:x=1.
(1)直接写出点B的坐标及一元二次方程ax2+bx﹣1.5=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的頂点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是CD的中点,点F是BC上的一点,且BF=3CF,连接AE、AF、EF,下列结论:①△ADE∽△ECF,②∠DAE=∠EAF,③AE2=ADAF,④S△AEF=5S△ECF,其中正确结论的个数是( )
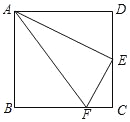
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
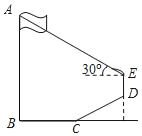
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
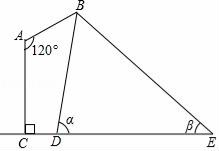
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 不经过第四象限,且与
不经过第四象限,且与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,其坐标为
上,其坐标为![]() ,连结
,连结![]() ,
,![]() ,若
,若![]() ,那么
,那么![]() 的值为( )
的值为( )
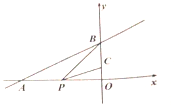
A. ![]() B. 4C. 5D. 6
B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
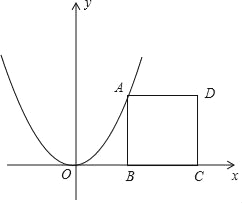
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com