
����Ŀ����ͼ1��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=13��BD=24��������ABCD���ⲿ��ABΪ�����ȱ������� ABE����F�ǶԽ���BD��һ���㣨��F�����B�غϣ������߶�AF�Ƶ�A˳ʱ�뷽����ת60���õ��߶�AM������FM��
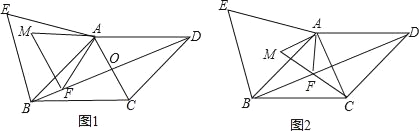
��1����AO�ij���
��2����ͼ2������F���߶�BO�ϣ��ҵ�M��F��C������ͬһ��ֱ����ʱ����֤��AC=![]() AM��
AM��
��3������EM������AEM�����Ϊ40����ֱ��д����AFM���ܳ���
���𰸡���1����5����2����֤�����̼���������3����3![]()
��������
�����������1������RT��OAB�У����ù��ɶ���OA=![]() ��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=
��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=![]() �����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=
�����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=![]() =
=![]() ���ó���AFM���ܳ�Ϊ3
���ó���AFM���ܳ�Ϊ3![]() ��
��
�����������1�������ı���ABCD�����Σ�
��AC��BD��OB=OD=![]() BD��
BD��
��BD=24��
��OB=12��
��Rt��OAB��
��AB=13��
��OA=![]() =5��
=5��
��2������ͼ2��
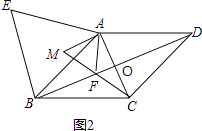
���ı���ABCD�����Σ�
��BD��ֱƽ��AC��
��FA=FC����FAC=��FCA��
����֪AF=AM����MAF=60����
���AFMΪ�ȱ������Σ�
���M=��AFM=60����
����M��F��C������ͬһ��ֱ���ϣ�
���FAC+��FCA=��AFM=60����
���FAC=��FCA=30����
���MAC=��MAF+��FAC=60��+30��=90����
��Rt��ACM����tan��M=![]() ��
��
��tan60��=![]() ��
��
��AC=![]() AM��
AM��
��3������ͼ������EM��
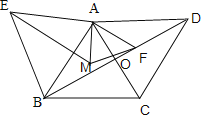
�ߡ�ABE�ǵȱ������Σ�
��AE=AB����EAB=60����
�ɣ�2��֪��AFMΪ�ȱ������Σ�
��AM=AF����MAF=60����
���EAM=��BAF��
����AEM����ABF�� ��
��
���AEM�ա�ABF��SAS����
�ߡ�AEM�����Ϊ40����ABF�ĸ�ΪAO
��![]() BFAO=40��BF=16��
BFAO=40��BF=16��
��FO=BF��BO=16��12=4
AF=![]() =
=![]() ��
��
���AFM���ܳ�Ϊ3![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
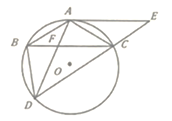
����Ŀ����ͼ����ƽ���ı���ABCD�У�����AC������ABC�����Բ��O���ӳ�EC����O�ڵ�D������BD��AD��BC��AD���ڵ�F�֣���ABC=��ADB��
��1����֤��AE�ǡ�O�����ߣ�
��2����AE=12��CD=10�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
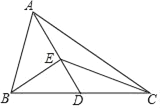
����Ŀ����֪����ͼ���ڡ�ABC�У�AB��9��BC��12����D��BC���е㣬����AD��AD��9����E��AD���ϣ���![]() ������BE��
������BE��
��1����֤����BED�ס�ABD��
��2������CE�����CED ������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�һ���Թ������������ÿ������ļ۸�������30Ԫ������2�������3��������340Ԫ��
(1)��ÿ�����������ļ۸�
(2)����Уһ���Թ������������60�����ܷ��ò�����3800Ԫ���ҹ�������ĸ�������39����������ĸ���Ϊm���ܷ���ΪyԪ��
����y����m�ĺ�����ϵʽ������m��ȡ������ֵ��
����ѧУ�������ķ�������ʱ��������ͣ���ͷ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȫУ1200��ѧ�����С�У��ȫ֪ʶ���Ľ��������1200��ѧ���������ȡ����ѧ�����в��ԣ��ɼ��������Ӹ߷ֵ��ͷ����з�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ĸ��ȼ���������ͼ�١�ͼ��������������ͳ��ͼ������ͼ��������Ϣ����������⣺
�ĸ��ȼ���������ͼ�١�ͼ��������������ͳ��ͼ������ͼ��������Ϣ����������⣺

��1���α�����ѧ�����ж�������
��2��������ͳ��ͼ������ͳ��ͼ����������
��3��������ͳ��ͼ�С�![]() �����ڵ�����Բ�ĽǵĶ�����
�����ڵ�����Բ�ĽǵĶ�����
��4������ȫУ��![]() ���ȼ���ѧ���ж�������
���ȼ���ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
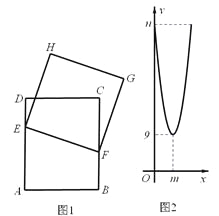
����Ŀ����ͼ1��A��B��C��DΪ���ε��ĸ����㣬AD=4cm��AB=dcm������E��F�ֱ�ӵ�D��B��������E��1 cm/s���ٶ��ر�DA���A�ƶ�����F��1 cm/s���ٶ��ر�BC���C�ƶ�����F�ƶ�����Cʱ������ͬʱֹͣ�ƶ�����EFΪ����������EFGH����F����xsʱ��������EFGH�����Ϊycm2����֪y��x�ĺ���ͼ���������ߵ�һ���֣���ͼ2��ʾ�������ͼ����Ϣ������������⣺
��1���Ա���x��ȡֵ��Χ�� �� ��
��2��d= �� ��m= �� ��n= �� ��
��3��F����������ʱ��������EFGH�����Ϊ16cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD����AB��AD����C��90������ABΪֱ���ġ�O��AD�ڵ�E��CD��ED������BD����O�ڵ�F��
��1����֤��BC����O���У�
��2����BD��10��AB��13����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ĵ�ʡ«ɽ��4��20�շ�����7.0��ǿ�ҵ�������Ϊ�˾����巿��������ij���´�������A�ְ��48000m2��B�ְ��24000m2������.
������ó�����280�����������ְ�ģ�ÿ��ÿ��������A�ְ��60 m2��B�ְ��40 m2�����ʣ�Ӧ�ֱ��Ŷ���������A�ְ�ĺ�B�ְ�ģ�����ȷ��ͬʱ��ɸ��Ե���������
��ij�����õ�ƻ��øó����������ְ�Ĵ�ס������ֹ��İ巿��400�䣬��֪����һ����Ͱ巿��һ�����Ͱ巿�����ļ������������±���ʾ��
�巿 | A�ְ��(m2) | B�ְ��(m2) | �������� |
���� | 110 | 61 | 12 |
���� | 160 | 53 | 10 |
�ٹ��ж����ֽ��������ɹ�ѡ��
������������õ���4700��������Ҫ���ã���400��巿�ܷ�������Ҫ��������������˵�����ɣ��������㣬��˵��Ӧѡ��ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABΪ��Oֱ����PQ���O���ڵ�C��AD��PQ�ڵ�D����ACΪ��DAB��ƽ���ߣ�BE��PQ�ڵ�E��
��1����֤��PQ���O���У�
��2����֤����C��DE���е㣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com