
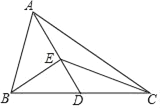
【题目】已知,如图,在△ABC中,AB=9,BC=12,点D是BC的中点,联结AD,AD=9,点E在AD边上,且![]() ,联结BE.
,联结BE.
(1)求证:△BED∽△ABD;
(2)联结CE,求∠CED 的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据AD=9, ![]() ,得到AE=5,DE=4,根据中点的性质得到BD=6,即可求出
,得到AE=5,DE=4,根据中点的性质得到BD=6,即可求出![]() 得到
得到![]() 又∠ADB=∠BDE,即可证明.
又∠ADB=∠BDE,即可证明.
(2)根据![]() BD=CD,得到
BD=CD,得到![]() 又ADC=∠CDE,得到△ADC∽△CDE,根据相似三角形的性质得到∠CED=∠ACB,过A作AH⊥BD于H,
又ADC=∠CDE,得到△ADC∽△CDE,根据相似三角形的性质得到∠CED=∠ACB,过A作AH⊥BD于H,
根据勾股定理得到![]() 即可求出tan∠CED=tan∠ACB=
即可求出tan∠CED=tan∠ACB=![]()
(1)证明:∵AD=9, ![]() ,
,
∴AE=5,DE=4,
∵BC=12,点D是BC的中点,
∴BD=6,
∵![]()
∴![]()
∵∠ADB=∠BDE,
∴△BED∽△ABD;
(2)∵![]() BD=CD,
BD=CD,
∴![]()
∵∠ADC=∠CDE,
∴△ADC∽△CDE,
∴∠CED=∠ACB,
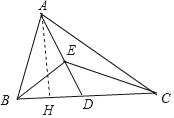
过A作AH⊥BD于H,
∵AB=AD=9,
∴BH=DH=3,
∴![]()
∴tan∠CED=tan∠ACB=![]()


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学报名参加学校运动会,有以下4个项目可供选择:
径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;
;
田赛项目:立定跳远![]() 用B表示
用B表示![]() .
.
![]() 小明从4个项目中任选一个,恰好是径赛项目的概率为______;
小明从4个项目中任选一个,恰好是径赛项目的概率为______;
![]() 小明从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
小明从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
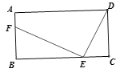
【题目】如图,在矩形ABCD中,AB=m,BC=8,E为线段BC上的动点(不与B,C重合),连接DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y,若![]() ,当DEF为等腰三角形时,m的值为_________.
,当DEF为等腰三角形时,m的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
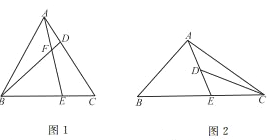
【题目】如图1,在△ABC中,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F。
(1)当∠ABC=∠C=60°时,![]() ,那么
,那么![]() ;(直接写出结论)
;(直接写出结论)
(2)当△ABC为等边三角形,![]() 时,请用含n的式子表示AF,BF的数量关系,并说明理由;
时,请用含n的式子表示AF,BF的数量关系,并说明理由;
(3)如图2,在△ABC中,∠ABC=45°,∠ACB=30°,AC=![]() ,点E在BC上,点D是AE的中点,当∠EDC=30°时,CE和DE的数量关系为。(直接写出结论,不必证明)
,点E在BC上,点D是AE的中点,当∠EDC=30°时,CE和DE的数量关系为。(直接写出结论,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,2),B(﹣2,﹣1),C(﹣1,﹣1),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
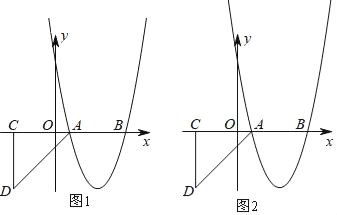
【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)过C(﹣3,0)向x轴下方作CD垂直x轴,连接AD,已知CD=4,将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点,试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
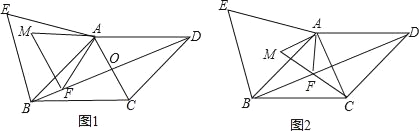
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
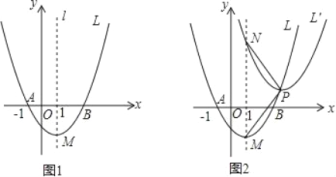
【题目】如图1,已知抛物线L:y=ax2+bx﹣1.5(a>0)与x轴交于点A(-1,0)和点B,顶点为M,对称轴为直线l:x=1.
(1)直接写出点B的坐标及一元二次方程ax2+bx﹣1.5=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的頂点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com