
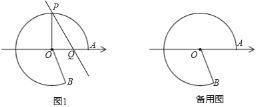
【题目】如图,点A在数轴上对应的数为20,以原点O为圆心,OA为半径作优弧![]() ,使点B在O右下方,且tan∠AOB=
,使点B在O右下方,且tan∠AOB=![]() ,在优弧
,在优弧![]() 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)若优弧上一段![]() 的长为10π,求∠AOP度数及x的值.
的长为10π,求∠AOP度数及x的值.
(2)若线段PQ的长为10,求这时x的值.
【答案】(1) ∠AOP=90°,x=![]() ;(2) x的值为
;(2) x的值为![]() 或﹣
或﹣![]() +5或
+5或![]() .
.
【解析】
(1)由![]() =10π,解得n=90°,即∠POQ=90°,在Rt△POQ中,OP=20,tan∠PQO=tan∠QOB=
=10π,解得n=90°,即∠POQ=90°,在Rt△POQ中,OP=20,tan∠PQO=tan∠QOB=![]() ,即可得出x的值;
,即可得出x的值;
解:(1)如图1,
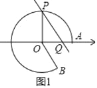
由![]() =10π,
=10π,
解得n=90°,
∴∠POQ=90°,
∵PQ∥OB,
∴∠PQO=∠BOQ,
∴tan∠PQO=tan∠QOB=![]() =
=![]()
∴OQ=![]()
∴x=![]() ;
;
(2)分三种情况:
①如图2,作OH⊥PQ于H,设OH=![]() k,QH=k.
k,QH=k.
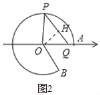
在Rt△OPH中,∵OP2=OH2+PH2,
∴202=(![]() k)2+(10﹣k)2,
k)2+(10﹣k)2,
整理得:k2﹣5k﹣75=0,
解得k=![]() 或k=
或k=![]() (舍弃),
(舍弃),
∴OQ=2k=![]()
此时x的值为![]()
②如图3,作OH⊥PQ交PQ的延长线于H.设OH=![]() k,QH=k.
k,QH=k.
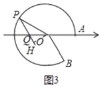
在Rt△在Rt△OPH中,∵OP2=OH2+PH2,
∴202=(![]() k)2+(10+k)2,
k)2+(10+k)2,
整理得:k2+5k﹣75=0,
解得k=![]() (舍弃)或k=
(舍弃)或k=![]() (舍弃),
(舍弃),
∴OQ=2k=![]() ,
,
此时x的值为﹣![]() +5
+5
③如图4,作OH⊥PQ于H,设OH=![]() k,QH=k.
k,QH=k.
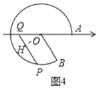
在Rt△OPH中,∵OP2=OH2+PH2,
∴202=(![]() k)2+(10﹣k)2,
k)2+(10﹣k)2,
整理得:k2﹣5k﹣75=0,
解得k=![]() 或
或![]() (舍弃),
(舍弃),
∴OQ=2k=![]()
此时x的值为![]() .
.
综上所述,满足条件的x的值为![]() 或﹣
或﹣![]() +5或
+5或![]() .
.


科目:初中数学 来源: 题型:
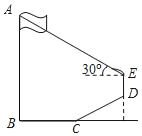
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
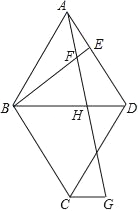
【题目】如图,菱形ABCD中,∠BAD=60°,点E在边AD上,连接BE,在BE上取点F,连接AF并延长交BD于H,且∠AFE=60°,过C作CG∥BD,直线CG、AF交于G.
(1)求证:∠FAE=∠EBA;
(2)求证:AH=BE;
(3)若AE=3,BH=5,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
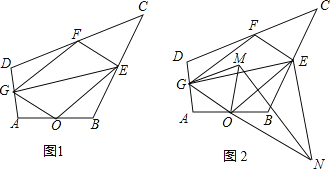
【题目】如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.
(1)证明:四边形OEFG是平行四边形;
(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.
①若OE=![]() ,OG=1,求
,OG=1,求![]() 的值;
的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
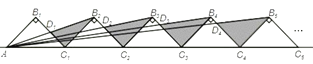
【题目】如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1Dnn的面积为Sn,则S1=_____;S2=_____;Sn=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
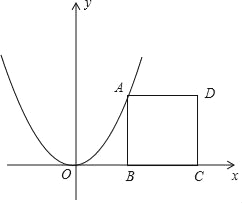
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
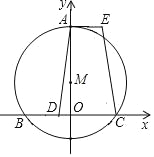
【题目】如图,在平面直角坐标系中,已知点M的坐标为(0,2),以M为圆心,以4为半径的圆与x轴相交于点B、C,与y轴正半轴相交于点A过A作AE∥BC,点D为弦BC上一点,AE=BD,连接AD,EC.
(1)求B、C两点的坐标;
(2)求证:AD=CE;
(3)若点P是弧BAC上一动点(P点与A、B点不重合),过点P的⊙M的切线PG交x轴于点G,若△BPG为直角三角形,试求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形AEFG均为菱形,且∠EAG=∠ABC.
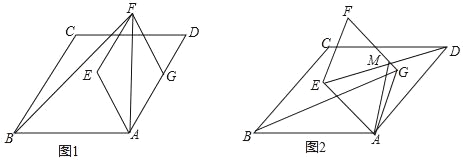
(1)如图1,点G在线段AD上,已知AD=5,AG=3,且cos∠ABC=![]()
![]() ,连接AF,BF,求BF的长;
,连接AF,BF,求BF的长;
(2)如图2,点G在菱形ABCD内部,连接BG、DE,若点M为DE中点,试猜想AM与BG之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com