
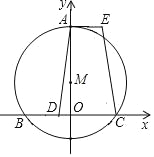
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌвдMЮЊдВаФЃЌвд4ЮЊАыОЖЕФдВгыxжсЯрНЛгкЕуBЁЂCЃЌгыyжсе§АыжсЯрНЛгкЕуAЙ§AзїAEЁЮBCЃЌЕуDЮЊЯвBCЩЯвЛЕуЃЌAEЃНBDЃЌСЌНгADЃЌECЃЎ
(1)ЧѓBЁЂCСНЕуЕФзјБъЃЛ
(2)ЧѓжЄЃКADЃНCEЃЛ
(3)ШєЕуPЪЧЛЁBACЩЯвЛЖЏЕу(PЕугыAЁЂBЕуВЛжиКЯ)ЃЌЙ§ЕуPЕФЁбMЕФЧаЯпPGНЛxжсгкЕуGЃЌШєЁїBPGЮЊжБНЧШ§НЧаЮЃЌЪдЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ
ЁОД№АИЁП(1)ЕуBЕФзјБъЮЊ(Љ2![]() ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2
ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2![]() ЃЌ0)ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2
ЃЌ0)ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2![]() ЃЌ4)ЃЌ(2
ЃЌ4)ЃЌ(2![]() ЃЌ4)ЃЎ
ЃЌ4)ЃЎ
ЁОНтЮіЁП
(1)ИљОнЙДЙЩЖЈРэПЩвдЧѓЕУOBКЭOCЕФГЄЖШЃЌДгЖјПЩвдЕУЕНBЁЂCСНЕуЕФзјБъЃЛ
(2)ИљОнЦНааЫФБпаЮЕФаджЪЁЂШЋЕШШ§НЧаЮЕФХаЖЈКЭаджЪПЩвджЄУїНсТлГЩСЂЃЛ
(3)ИљОнЬтвтЃЌЛГіЯргІЕФЭМаЮЃЌШЛКѓРћгУЗжРрЬжТлЕФЗНЗЈПЩвдЕУЕНЕуPЕФзјБъЃЎ
НтЃК(1)СЌНгMBЁЂMCЃЌШчЭМвЛЫљЪОЃЌ
ЁпЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌвдMЮЊдВаФЃЌвд4ЮЊАыОЖЕФдВгыxжсЯрНЛгкЕуBЁЂCЃЌ
ЁрMBЃНMCЃН4ЃЌOMЃН2ЃЌ
ЁпЁЯMOBЃНЁЯMOCЃН90ЁуЃЌ
ЁрOBЃН![]() ЃЌ
ЃЌ
ЁрOCЃН2![]() ЃЌ
ЃЌ
ЁрЕуBЕФзјБъЮЊ(Љ2![]() ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2
ЃЌ0)ЃЌЕуCЕФзјБъЮЊ(2![]() ЃЌ0)ЃЛ
ЃЌ0)ЃЛ
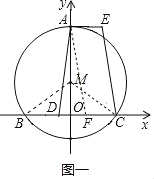
(2)жЄУїЃКзїAFЁЮECНЛxжсгкЕуFЃЌШчЭМвЛЫљЪОЃЌ
ЁпAEЁЮBCЃЌ
ЁрЫФБпаЮAFCEЪЧЦНааЫФБпаЮЃЌ
ЁрAEЃНFCЃЌAFЃНECЃЌ
ЁпAEЃНBDЃЌ
ЁрBDЃНCFЃЌ
гжЁпOBЃНOCЃЌ
ЁрODЃНOFЃЌ
дкЁїAODКЭЁїAOFжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїAODЁеЁїAOF(SAS)ЃЌ
ЁрADЃНAFЃЌ
ЁрADЃНECЃЌ
МДADЃНCEЃЛ
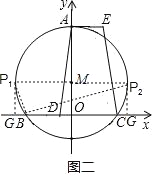
(3)ЕБЁїBP1GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМЖўЫљЪОЃЌ
ЁпMAЃНMP1ЃН4ЃЌЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌ
ЁрЕуP1ЕФзјБъЮЊ(Љ4ЃЌ2)ЃЛ
ЕБЁїBP2GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМЖўЫљЪОЃЌ
ЁпMAЃНMP2ЃН4ЃЌЕуMЕФзјБъЮЊ(0ЃЌ2)ЃЌ
ЁрЕуP2ЕФзјБъЮЊ(4ЃЌ2)ЃЛ
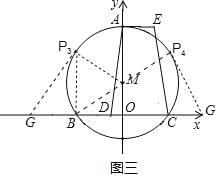
ЕБЁїBP3GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМШ§ЫљЪОЃЌ
ЁпOBЃН2![]() ЃЌOMЃН2ЃЌ
ЃЌOMЃН2ЃЌ
ЁрtanЁЯMBOЃН![]() ЃЌ
ЃЌ
ЁрЁЯMBOЃН30ЁуЃЌ
ЁрЁЯMBP3ЃН60ЁуЃЌ
ЁпBMЃНMP3ЃЌ
ЁрЁїBMP3ЪЧЕШБпШ§НЧаЮЃЌ
ЁрBP3ЃН4ЃЌ
ЁрЕуP3ЕФзјБъЮЊ(Љ2![]() ЃЌ4)ЃЛ
ЃЌ4)ЃЛ
ЕБЁїBP4GЪЧжБНЧШ§НЧаЮЪБЃЌШчЭМШ§ЫљЪОЃЌ
ЁпBP4ЃН8ЃЌЁЯP4BGЃН30ЁуЪБЃЌ
ЁрЕуP4ЕФзнзјБъЪЧЃК8ЁСsin30ЁуЃН8ЁС![]() ЃН4ЃЌКсзјБъЪЧЃКЉ2
ЃН4ЃЌКсзјБъЪЧЃКЉ2![]() +8ЁСcos30ЁуЃНЉ2
+8ЁСcos30ЁуЃНЉ2![]() +8ЁС
+8ЁС![]() ЃНЉ2
ЃНЉ2![]() +4
+4![]() ЃН2
ЃН2![]() ЃЌ
ЃЌ
ЁрЕуP4ЕФзјБъЮЊ(2![]() ЃЌ4)ЃЛ
ЃЌ4)ЃЛ
гЩЩЯПЩЕУЃЌШєЁїBPGЮЊжБНЧШ§НЧаЮЃЌЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЪЧ(Љ4ЃЌ2)ЃЌ(4ЃЌ2)ЃЌ(Љ2![]() ЃЌ4)ЃЌ(2
ЃЌ4)ЃЌ(2![]() ЃЌ4)ЃЎ
ЃЌ4)ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬхг§ПЮЩЯЃЌаЁУїЁЂаЁЧПЁЂаЁЛЊШ§ШЫдкзуЧђГЁЩЯСЗЯАзуЧђДЋЧђЃЌзуЧђДгвЛИіШЫДЋЕНСэвЛИіШЫМЧЮЊЬпвЛДЮЃЎШчЙћДгаЁЧППЊЪМЬпЃЌОЙ§СНДЮЬпЧђКѓЃЌзуЧђЬпЕНаЁЛЊДІЕФИХТЪЪЧЖрЩйЃПОЙ§Ш§ДЮЬпЧђКѓЃЌзуЧђЬпЛиЕНаЁЧПДІЕФИХТЪФиЃПЃЈСаБэЛђЛЪїаЮЭМЛђСаОйЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAдкЪ§жсЩЯЖдгІЕФЪ§ЮЊ20ЃЌвддЕуOЮЊдВаФЃЌOAЮЊАыОЖзїгХЛЁ![]() ЃЌЪЙЕуBдкOгвЯТЗНЃЌЧвtanЁЯAOBЃН
ЃЌЪЙЕуBдкOгвЯТЗНЃЌЧвtanЁЯAOBЃН![]() ЃЌдкгХЛЁ
ЃЌдкгХЛЁ![]() ЩЯШЮШЁвЛЕуPЃЌЧвФмЙ§PзїжБЯпlЁЮOBНЛЪ§жсгкЕуQЃЌЩшQдкЪ§жсЩЯЖдгІЕФЪ§ЮЊxЃЌСЌНгOPЃЎ
ЩЯШЮШЁвЛЕуPЃЌЧвФмЙ§PзїжБЯпlЁЮOBНЛЪ§жсгкЕуQЃЌЩшQдкЪ§жсЩЯЖдгІЕФЪ§ЮЊxЃЌСЌНгOPЃЎ
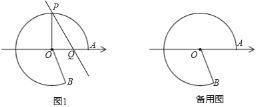
ЃЈ1ЃЉШєгХЛЁЩЯвЛЖЮ![]() ЕФГЄЮЊ10ІаЃЌЧѓЁЯAOPЖШЪ§МАxЕФжЕЃЎ
ЕФГЄЮЊ10ІаЃЌЧѓЁЯAOPЖШЪ§МАxЕФжЕЃЎ
ЃЈ2ЃЉШєЯпЖЮPQЕФГЄЮЊ10ЃЌЧѓетЪБxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФаЁе§ЗНаЮЭјИёжаЃЌЕуAЁЂBЁЂCЁЂDЖМдкетаЉаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌABЁЂCDЯрНЛгкЕуOЃЌдђtanЁЯAOD=________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЮЊЖўДЮКЏЪ§yЃНax2+bx+cЕФЭМЯѓЃЌдкЯТСаЫЕЗЈжаЂйacЃО0ЃЛЂкЗНГЬax2+bx+cЃН0ЕФИљЪЧx1ЃНЉ1ЃЌx2ЃН3ЃЛЂлa+b+cЃМ0ЃЛЂмЕБxЃО1ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌе§ШЗЕФЪЧ( )
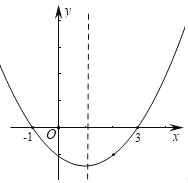
A. ЂйЂлB. ЂкЂмC. ЂйЂкЂмD. ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
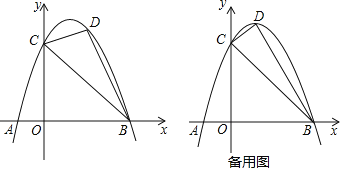
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛxжсгкAЁЂBСНЕу
ЕФЭМЯѓНЛxжсгкAЁЂBСНЕу![]() ЦфжаЕуAдкЕуBЕФзѓВр
ЦфжаЕуAдкЕуBЕФзѓВр![]() ЃЌНЛyжсе§АыжсгкЕуCЃЌЧв
ЃЌНЛyжсе§АыжсгкЕуCЃЌЧв![]() ЃЌЕуDдкИУКЏЪ§ЕФЕквЛЯѓЯоФкЕФЭМЯѓЩЯЃЎ
ЃЌЕуDдкИУКЏЪ§ЕФЕквЛЯѓЯоФкЕФЭМЯѓЩЯЃЎ
![]() ЧѓЕуAЁЂЕуBЕФзјБъЃЛ
ЧѓЕуAЁЂЕуBЕФзјБъЃЛ
![]() Шє
Шє![]() ЕФзюДѓУцЛ§ЮЊ
ЕФзюДѓУцЛ§ЮЊ![]() ЦНЗНЕЅЮЛЃЌЧѓЕуDЕФзјБъМАЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
ЦНЗНЕЅЮЛЃЌЧѓЕуDЕФзјБъМАЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
![]() ШєЕуDЮЊИУКЏЪ§ЭМЯѓЕФЖЅЕуЃЌЧв
ШєЕуDЮЊИУКЏЪ§ЭМЯѓЕФЖЅЕуЃЌЧв![]() ЪЧжБНЧШ§НЧаЮЃЌЧѓДЫЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЎ
ЪЧжБНЧШ§НЧаЮЃЌЧѓДЫЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊОиаЮPMONЕФБпOMЁЂONЗжБ№дкxЁЂyжсЩЯЃЌOЮЊзјБъдЕуЃЌЧвЕуPЕФзјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЎНЋОиаЮPMONбиxжсе§ЗНЯђЦНвЦ4ИіЕЅЮЛЃЌЕУЕНОиаЮP1M1O1N1дйНЋОиаЮP1M1O1N1ШЦзХЕуO1а§зЊ90ЁуЕУЕНОиаЮP2M2O2N2ЃЎдкзјБъЯЕжаЛГіОиаЮP2M2O2N2ЃЌВЂЧѓГіжБЯпP1P2ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
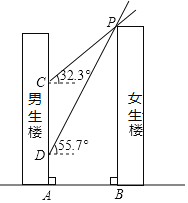
ЁОЬтФПЁПШчЭМЃЌФаЩњТЅдкХЎЩњТЅЕФзѓВрЃЌСНТЅИпЖШОљЮЊ90mЃЌТЅМфОрЮЊABЃЌЖЌжСШее§ЮчЃЌЬЋбєЙтЯпгыЫЎЦНУцЫљГЩЕФНЧЮЊ![]() ЃЌХЎЩњТЅдкФаЩњТЅЧНУцЩЯЕФгАИпЮЊCAЃЛДКЗжШее§ЮчЃЌЬЋбєЙтЯпгыЫЎЦНУцЫљГЩЕФНЧЮЊ
ЃЌХЎЩњТЅдкФаЩњТЅЧНУцЩЯЕФгАИпЮЊCAЃЛДКЗжШее§ЮчЃЌЬЋбєЙтЯпгыЫЎЦНУцЫљГЩЕФНЧЮЊ![]() ЃЌХЎЩњТЅдкФаЩњТЅЧНУцЩЯЕФгАИпЮЊDAЃЌвбжЊ
ЃЌХЎЩњТЅдкФаЩњТЅЧНУцЩЯЕФгАИпЮЊDAЃЌвбжЊ![]() ЃЎ
ЃЎ
![]() ЧѓТЅМфОрABЃЛ
ЧѓТЅМфОрABЃЛ
![]() ШєФаЩњТЅЙВ30ВуЃЌВуИпОљЮЊ3mЃЌЧыЭЈЙ§МЦЫуЫЕУїЖрЩйВувдЯТЛсЪмЕНЕВЙтЕФгАЯьЃП
ШєФаЩњТЅЙВ30ВуЃЌВуИпОљЮЊ3mЃЌЧыЭЈЙ§МЦЫуЫЕУїЖрЩйВувдЯТЛсЪмЕНЕВЙтЕФгАЯьЃП![]() ВЮПМЪ§ОнЃК
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНЉx2+bx+cОЙ§ЕуBЃЈЉ1ЃЌ0ЃЉКЭЕуCЃЈ2ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШчЙћДЫХзЮяЯпЩЯЯТЦНвЦКѓЙ§ЕуЃЈЉ2ЃЌЉ1ЃЉЃЌЪдШЗЖЈЦНвЦЕФЗНЯђКЭЦНвЦЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com