
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而增大,正确的是( )
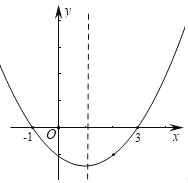
A. ①③B. ②④C. ①②④D. ②③④
科目:初中数学 来源: 题型:
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
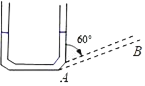
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1Dnn的面积为Sn,则S1=_____;S2=_____;Sn=_____.
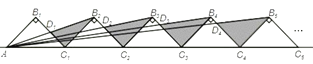
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
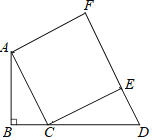
【题目】如图,四边形ACEF为正方形,以AC为斜边作Rt△ABC,∠B=90°,AB=4,BC=2,延长BC至点D,使CD=5,连接DE.
(1)求正方形的边长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
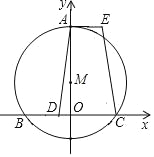
【题目】如图,在平面直角坐标系中,已知点M的坐标为(0,2),以M为圆心,以4为半径的圆与x轴相交于点B、C,与y轴正半轴相交于点A过A作AE∥BC,点D为弦BC上一点,AE=BD,连接AD,EC.
(1)求B、C两点的坐标;
(2)求证:AD=CE;
(3)若点P是弧BAC上一动点(P点与A、B点不重合),过点P的⊙M的切线PG交x轴于点G,若△BPG为直角三角形,试求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:制作无盖盒子
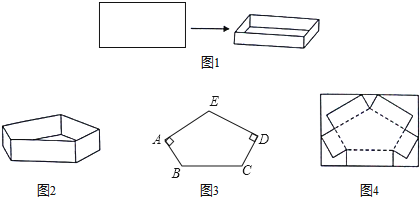
任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为![]() 的无盖长方体盒子
的无盖长方体盒子![]() 纸板厚度忽略不计
纸板厚度忽略不计![]() .
.
![]() 请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
![]() 请求出这块矩形纸板的长和宽.
请求出这块矩形纸板的长和宽.
任务二:图2是一个高为4cm的无盖的五棱柱盒子![]() 直棱柱
直棱柱![]() ,图3是其底面,在五边形ABCDE中,
,图3是其底面,在五边形ABCDE中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 试判断图3中AE与DE的数量关系,并加以证明.
试判断图3中AE与DE的数量关系,并加以证明.
![]() 图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果
图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果![]() 图中实线表示剪切线,虚线表示折痕
图中实线表示剪切线,虚线表示折痕![]() 纸板厚度及剪切接缝处损耗忽略不计
纸板厚度及剪切接缝处损耗忽略不计![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com