
【题目】如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A
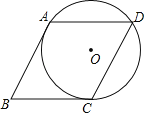
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
【答案】解:(1)证明:如图,连接OA、OB、OC,
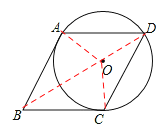
∵AB与⊙O切于A点,∴OA⊥AB,即∠OAB=90°。
∵四边形ABCD为菱形,∴BA=BC。
在△ABO和△CBO中,∵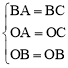 ,
,
∴△ABC≌△CBO(SSS)。∴∠BOC=∠OAC=90°。∴OC⊥BC。
∵OC是⊙O的半径,∴BC为⊙O的切线。
(2)连接BD,
∵△ABC≌△CBO,∴∠AOB=∠COB。
∵四边形ABCD为菱形,∴BD平分∠ABC,CB=CD。
∴点O在BD上。
∵∠BOC=∠ODC+∠OCD,而OD=OC,∴∠ODC=∠OCD。
∴∠BOC=2∠ODC。
∵CB=CD,∴∠OBC=∠ODC。∴∠BOC=2∠OBC。
∵∠BOC+∠OBC=90°,∴∠OBC=30°。∴∠ABC=2∠OBC=60°
【解析】
试题(1)连接OA、OB、OC、BD,根据切线的性质得OA⊥AB,即∠OAB=90°,再根据菱形的性质得BA=BC,然后根据“SSS”可判断△ABC≌△CBO,则∠BOC=∠OAC=90°,于是可根据切线的判定方法即可得到结论。
(2)由△ABC≌△CBO得∠AOB=∠COB,则∠AOB=∠COB,由于菱形的对角线平分对角,所以点O在BD上,利用三角形外角性质有∠BOC=∠ODC+∠OCD,则∠BOC=2∠ODC,由于CB=CD,则∠OBC=∠ODC,所以∠BOC=2∠OBC,根据∠BOC+∠OBC=90°可计算出∠OBC=30°,然后利用∠ABC=2∠OBC计算即可。


科目:初中数学 来源: 题型:
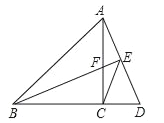
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=10,BC=6,点D在AB的延长线上,且BD=6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径;
(2)设CD交⊙O于点Q,①试说明Q为CD的中点;②求BQ·BE的值.
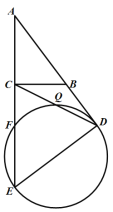
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
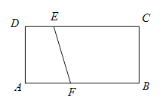
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 是两个全等的直角三角形,量得它们的斜边长为
是两个全等的直角三角形,量得它们的斜边长为![]() ,较小锐角为
,较小锐角为![]() ,将这两个三角形摆成如图(1)所示的形状,使点
,将这两个三角形摆成如图(1)所示的形状,使点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,且点
在同一条直线上,且点![]() 与点
与点![]() 重合,将图(1)中的
重合,将图(1)中的![]() 绕点
绕点![]() 顺时针方向旋转到图(2)的位置,点
顺时针方向旋转到图(2)的位置,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______
的长为______![]() .(保留根号)
.(保留根号)
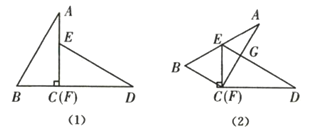
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )

A.150°B.135°C.120°D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com