
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
【答案】0或1<AF< ![]() 或4
或4
【解析】
学习了圆周角的推论: 直径所对的圆周角是直角, 可提供解题思路, 可以以EF为直径作圆, 以边界值去讨论该圆与矩形ABCD交点的个数.
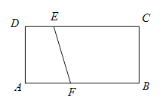
解:以EF为斜边的直角三角形的直角顶点P是以EF为直径的圆与矩形边的交点, 取EF的中点O,
(1) 如图1, 当圆O与AD相切于点G时, 连结OG, 此时点G与点P重合,只有一个点, 此时AF=OG=DE=1;

(2) 如图2, 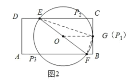
当圆O与BC相切于点G, 连结OG,EG, FG, 此时有三个点P可以构成Rt△EFP,
![]() OG是圆O的切线,
OG是圆O的切线,![]() OG⊥BC
OG⊥BC
![]() OG∥AB∥CD
OG∥AB∥CD
![]() OE=OF,
OE=OF,
![]() BG=CG,
BG=CG,![]() OG=
OG=![]() (BF+CE),
(BF+CE),
设AF=x, 则BF=4-x, OG=![]() (4-x+4-1)=
(4-x+4-1)= ![]() (7-x)
(7-x)
则EF=20G=7-x, EG![]() =EC
=EC![]() +CG
+CG![]() =9+1=10,FG
=9+1=10,FG![]() =BG
=BG![]() +BF
+BF![]() =1+(4-x)
=1+(4-x)![]() ,
,
在Rt△EFG中, 由勾股定理得EF![]() =EG
=EG![]() +FG
+FG![]() ,
,
得(7-x)![]() =10+1+(4-x)2,解得x=
=10+1+(4-x)2,解得x=![]() ,
,
所以当1<AF<![]() 时,以EF为直径的圆与矩形ABCD的交点 (除了点E和F) 只有两个;
时,以EF为直径的圆与矩形ABCD的交点 (除了点E和F) 只有两个;
(3)因为点F是边AB上一动点:
当点F与A点重合时, AF=4, 此时Rt△EFP正好有两个符合题意;
故答案为0或1<AF< ![]() 或4.
或4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣![]() )2=
)2=![]()
D.3x2﹣4x﹣2=0化为(x﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
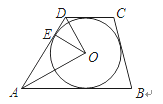
【题目】如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(1)求证:AO2=AEAD;
(2)若AO=4cm,AD=5cm,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
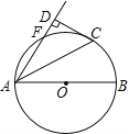
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且点C为弧BF的中点,连接AC、AF,过点C作CD⊥AF交AF延长线于点D.
(1)求证:CD是⊙O的切线;
(2)判断线段AB、AF与AD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)画出![]() 关于原点对称的三角形
关于原点对称的三角形![]() ;
;
(2)将三角形![]() 、
、![]() 、
、![]() 绕坐标原点
绕坐标原点![]() 逆时针旋转
逆时针旋转![]() ,画出图形,直接写出
,画出图形,直接写出![]() 的对应点的坐标.
的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有![]() 个,黑球有
个,黑球有![]() 个,绿球有
个,绿球有![]() 个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某陶瓷公司招工广告称:“本公司工人工作时间:每天工作![]() 小时,每月工作
小时,每月工作![]() 天;待遇:工人按计件付工资,每月另加生活费
天;待遇:工人按计件付工资,每月另加生活费![]() 元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
甲种陶瓷 (单位:个) | 乙种陶瓷 (单位:个) | 总时间 (单位:分钟) | 计件工资 (单位:元) |
|
|
|
|
|
|
|
|
(1)设生产每个甲种陶瓷所需的时间为![]() 分钟,用含有
分钟,用含有![]() 的代数式表示生产每个乙种陶瓷所需的时间;
的代数式表示生产每个乙种陶瓷所需的时间;
(2)设小王工人小王某月(工作![]() 天)生产甲种陶瓷
天)生产甲种陶瓷![]() 个,乙种陶瓷
个,乙种陶瓷![]() 个,
个,
①试求![]() 与
与![]() 的函数关系式;(不需写出自变量
的函数关系式;(不需写出自变量![]() 的取值范围)
的取值范围)
②根据市场调查,每个工人每月生产甲种陶瓷的数量不少于乙种陶瓷数量的![]() 倍,且生产每个乙种陶瓷的计件工资可提高
倍,且生产每个乙种陶瓷的计件工资可提高![]() 元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资
元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资![]() 月工资)才能领到
月工资)才能领到![]() 元?
元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com