
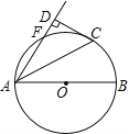
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且点C为弧BF的中点,连接AC、AF,过点C作CD⊥AF交AF延长线于点D.
(1)求证:CD是⊙O的切线;
(2)判断线段AB、AF与AD之间的数量关系,并说明理由.
【答案】(1)证明见解析;(2)AF+AB=2AD ,理由见解析.
【解析】
(1)由![]() =
=![]() ,OA=OC知∠DAC=∠BAC=∠ACO,由CD⊥AF知∠DAC+∠DCA=90°,从而得∠DCO=90°,从而得证;
,OA=OC知∠DAC=∠BAC=∠ACO,由CD⊥AF知∠DAC+∠DCA=90°,从而得∠DCO=90°,从而得证;
(2)作CE⊥AB,连接CF,CB,先证Rt△DAC≌Rt△EAC得AD=AE,再证Rt△CDF≌Rt△CEB得DF=EB,根据AF=AD﹣CF,AB=AE+BE可得答案.
(1)连接OC.
∵![]() =
=![]() ,OA=OC,∴∠DAC=∠BAC=∠ACO.
,OA=OC,∴∠DAC=∠BAC=∠ACO.
∵CD⊥AF于D,∴∠DAC+∠DCA=90°,∴∠DCA+∠OCA=90°,即∠DCO=90°,∴CD为⊙O的切线.
(2)AF+AB=2AD.理由如下:
过C点作CE⊥AB于E,连接CF,CB,则∠CDA=∠CEA=90°.
∵∠DAC=∠EAC,AC=AC,∴Rt△DAC≌Rt△EAC(AAS),CD=CE,AD=AE.
又∵∠DFC+∠AFC=180°,∠AFC+∠B=180°,∴∠DFC=∠B,∴Rt△CDF≌Rt△CEB(AAS),∴DF=EB,∴AF=AD﹣CF,AB=AE+BE,∴AF+AB=AD+AE=2AD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象在一,三象限.
(m为常数)的图象在一,三象限.
(1)求m的取值范围;
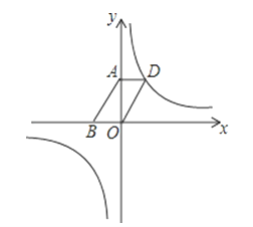
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,4),(﹣3,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且分别交
且分别交![]() 轴负半轴、直线
轴负半轴、直线![]() 于点
于点![]() 、
、![]() ,
,![]() .
.
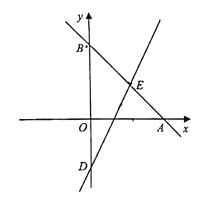
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)若点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
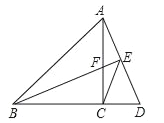
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)
甲:5、6、7、9、8
乙:8、4、8、6、9
(1)分别计算这两组数据的平均数和方差;
(2)根据测试成绩,你认为选派哪一名选手参赛更好些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
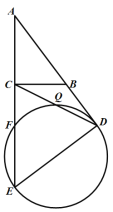
【题目】如图,在△ABC中,∠ACB=90°,AB=10,BC=6,点D在AB的延长线上,且BD=6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径;
(2)设CD交⊙O于点Q,①试说明Q为CD的中点;②求BQ·BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
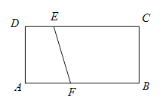
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )

A.150°B.135°C.120°D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车间同时开始加工一批服装,从开始加工到完成这批服装甲车间工作了8小时,乙车间在中途停工一段时间维修设备,然后在甲车间加工到4小时时按停工前的工作效率继续加工,直至与甲车间同时完成这批服装的加工任务.设甲、乙两车间各自加工服装的数量为![]() (件),甲车间加工的时间为
(件),甲车间加工的时间为![]() (时),
(时),![]() 与
与![]() 的函数图象如图所示.
的函数图象如图所示.
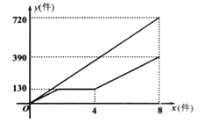
(1)甲车间每小时加工服装的件数为________件,这批服装的总件数为________件;
(2)乙车间花了多少时间维修设备?
(3)求甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com