
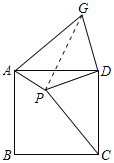
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )

A.150°B.135°C.120°D.108°
【答案】B
【解析】
连接PG,由题意得出PD=GD=2,∠CDP=∠ADG,得出∠PDG=∠ADC=90°,得出△PDG是等腰直角三角形,由等腰直角三角形的性质得出∠GPD=45°,PG=![]() PD=2
PD=2![]() ,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
,得出AP2+PG2=AG2,由勾股定理的逆定理得出∠GPA=90°,即可得出答案.
解:连接PG,如图所示:
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,AG=PC=3,
∵PA=1,PD=2,PC=3,将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),
∴PD=GD=2,∠CDP=∠ADG,
∴∠PDG=∠ADC=90°,
∴△PDG是等腰直角三角形,
∴∠GPD=45°,PG=![]() PD=2
PD=2![]() ,
,
∵AG=PC=3,AP=1,PG=2![]() ,
,
∴AP2+PG2=AG2,
∴∠GPA=90°,
∴∠APD=90°+45°=135°;
故选:B.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一个粒子在![]() 轴上及第一象限内运动,第1次从
轴上及第一象限内运动,第1次从![]() 运动到
运动到![]() ,第2次从
,第2次从![]() 运动到
运动到![]() ,第3次从
,第3次从![]() 运动到
运动到![]() ,它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )
,它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
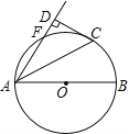
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且点C为弧BF的中点,连接AC、AF,过点C作CD⊥AF交AF延长线于点D.
(1)求证:CD是⊙O的切线;
(2)判断线段AB、AF与AD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
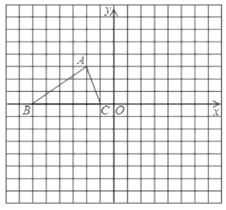
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)画出![]() 关于原点对称的三角形
关于原点对称的三角形![]() ;
;
(2)将三角形![]() 、
、![]() 、
、![]() 绕坐标原点
绕坐标原点![]() 逆时针旋转
逆时针旋转![]() ,画出图形,直接写出
,画出图形,直接写出![]() 的对应点的坐标.
的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有![]() 个,黑球有
个,黑球有![]() 个,绿球有
个,绿球有![]() 个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某校对各个班级的教室卫生检查成绩如下表所示:
地面 | 门窗 | 桌椅 | 黑板 | |
一班 |
|
|
|
|
二班 |
|
|
|
|
三班 |
|
|
|
|
(1)若按平均成绩计算,哪班卫生成绩最好?
(2)若将地面、门窗、桌椅、黑板按![]() ,
,![]() ,
,![]() ,
,![]() 的比例计算各班卫生成绩,那么哪个班的成绩最高?
的比例计算各班卫生成绩,那么哪个班的成绩最高?
(3)试统计你校八年级各个班地面、门窗、桌椅、黑板的卫生成绩,并分别按(1)、(2)的评分标准计算成绩,看看你所在班级的卫生情况,你将怎样继续改进?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.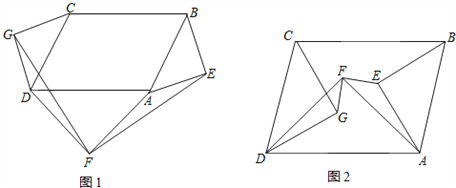
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com