
【题目】如图,平面直角坐标系中,点![]() 都在
都在![]() 轴上,点
轴上,点![]() 都在直线
都在直线![]() 上,
上,![]() ,且
,且![]() ,分别是以
,分别是以![]() 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则![]() 的面积是_______.
的面积是_______.

科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-3过A(-1,0)、B(3,0),直线AD交抛物线于点D,点D的横坐标为2,点P(m,n)是线段AD上的动点.
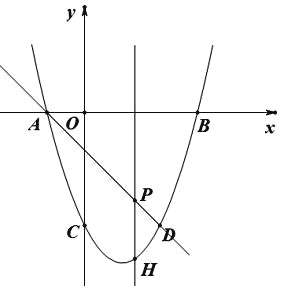
(1)求直线AD及抛物线的解析式.
(2)过点P的直线垂直于x轴,交抛物线于点H,求线段PH的长度l与m的关系式,m为何值时,PH最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)E,使得P、H、D、E为顶点的四边形是平行四边形?若存在,请求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=10,BC=6,点D在AB的延长线上,且BD=6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径;
(2)设CD交⊙O于点Q,①试说明Q为CD的中点;②求BQ·BE的值.
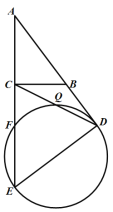
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 是两个全等的直角三角形,量得它们的斜边长为
是两个全等的直角三角形,量得它们的斜边长为![]() ,较小锐角为
,较小锐角为![]() ,将这两个三角形摆成如图(1)所示的形状,使点
,将这两个三角形摆成如图(1)所示的形状,使点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,且点
在同一条直线上,且点![]() 与点
与点![]() 重合,将图(1)中的
重合,将图(1)中的![]() 绕点
绕点![]() 顺时针方向旋转到图(2)的位置,点
顺时针方向旋转到图(2)的位置,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______
的长为______![]() .(保留根号)
.(保留根号)
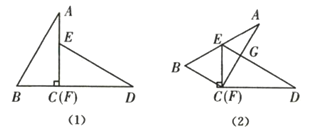
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )

A.150°B.135°C.120°D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
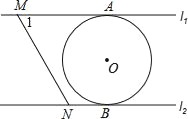
A. MN=![]() B. 若MN与⊙O相切,则AM=
B. 若MN与⊙O相切,则AM=![]()
C. l1和l2的距离为2 D. 若∠MON=90°,则MN与⊙O相切
查看答案和解析>>
科目:初中数学 来源: 题型:
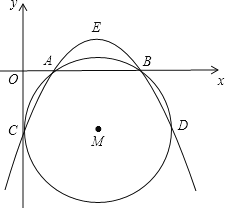
【题目】如图,在直角坐标系中,抛物线y=a(x-![]() )2+
)2+![]() 与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
(1)求a值及A,B两点坐标;
(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角时,请求出m的取值范围;
(3)点E是抛物线的顶点,⊙M沿CD所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com