
【题目】如图,在直角坐标系中,抛物线y=a(x-![]() )2+
)2+![]() 与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
(1)求a值及A,B两点坐标;
(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角时,请求出m的取值范围;
(3)点E是抛物线的顶点,⊙M沿CD所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.
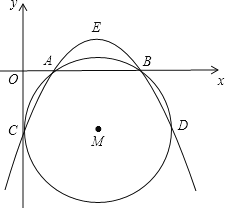
【答案】(1)A(1,0),B(4,0).(2)m<0或1<m<4或m>5.(3)存在.M′(![]() ,-2)
,-2)
【解析】
(1)把点C坐标代入抛物线解析式即可求出a,令y=0可得抛物线与x轴的交点坐标.
(2)根据题意可知,当点P在圆外部的抛物线上运动时,∠CPD为锐角,由此即可解决问题.
(3)存在.如图2中,将线段C'A平移至D'F,当点D'与点H重合时,四边形AC'D'E的周长最小,求出点H坐标即可解决问题.
解:(1)∵抛物线y=a(x-![]() )2+
)2+![]() 经过点C(0,-2),
经过点C(0,-2),
∴-2=a(0-![]() )2+
)2+![]() ,
,
∴a=-![]() ,
,
∴y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
当y=0时,-![]() (x-
(x-![]() )2+
)2+![]() =0,
=0,
∴x1=4,x2=1,
∵A、B在x轴上,
∴A(1,0),B(4,0).
(2)由(1)可知抛物线解析式为y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴C、D关于对称轴x=![]() 对称,
对称,
∵C(0,-2),
∴D(5,-2),
如图1中,连接AD、AC、CD,则CD=5,
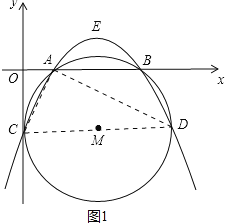
∵A(1,0),C(0,-2),D(5,-2),
∴AC=![]() ,AD=2
,AD=2![]() ,
,
∴AC2+AD2=CD2,
∴∠CAD=90°,
∴CD为⊙M的直径,
∴当点P在圆外部的抛物线上运动时,∠CPD为锐角,
∴m<0或1<m<4或m>5.
(3)存在.如图2中,将线段C′A平移至D′F,则AF=C′D′=CD=5,
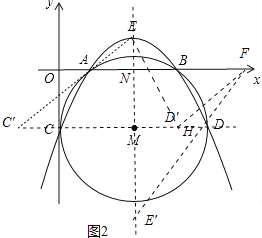
∵A(1,0),
∴F(6,0),
作点E关于直线CD的对称点E′,
连接EE′正好经过点M,交x轴于点N,
∵抛物线顶点(![]() ,
,![]() ),直线CD为y=-2,
),直线CD为y=-2,
∴E′(![]() ,-
,-![]() ),
),
连接E′F交直线CD于H,
∵AE,C′D′是定值,
∴AC′+ED′最小时,四边形AC′D′E的周长最小,
∵AC′+D′E=FD′+D′E=FD′+E′D′≥E′F,
则当点D′与点H重合时,四边形AC′D′E的周长最小,
设直线E′F的解析式为y=kx+b,
∵E′(![]() ,-
,-![]() ),F(6,0),
),F(6,0),
∴可得y=![]() x-
x-![]() ,
,
当y=-2时,x=![]() ,
,
∴H(![]() ,-2),∵M(
,-2),∵M(![]() ,-2),
,-2),
∴DD′=5-![]() =
=![]() ,
,
∵![]() -
-![]() =
=![]() ,
,
∴M′(![]() ,-2)
,-2)


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车从A地驶向B地,甲车比乙车早出发2h,并且甲车在途中休息了0.5h,甲、乙两车离A地的距离y(km)与甲车行驶时间x(h)之间的函数图象如图所示.根据图象提供的信息,下列说法:
①乙车速度比甲车慢;②a=40;③乙车比甲车早1.75小时到达B地.
其中正确的有( )
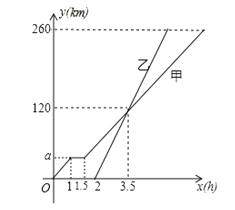
A.0个B.2个C.1个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.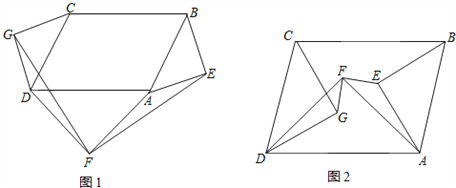
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 均是等边三角形,点
均是等边三角形,点![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ﹔④
﹔④![]() ,其中正确结论有_________个.
,其中正确结论有_________个.
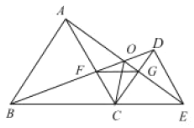
查看答案和解析>>
科目:初中数学 来源: 题型:
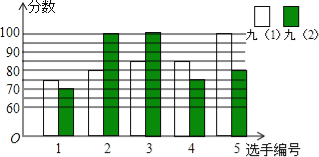
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | 85 | |
九(2) | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子,镜子的长与宽的比是2:1,设制作这面镜子的宽度是x米,总费用是y元,则y=240x2+180x+60.(注:总费用=镜面玻璃的费用+边框的费用+加工费).
(1)这块镜面玻璃的价格是每平方米 元,加工费 元;
(2)如果制作这面镜子共花了210元,求这面镜子的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐角系中,点![]() 是原点,点
是原点,点![]() 、
、![]() 在坐标轴上,连接
在坐标轴上,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 是线段
是线段![]() 的垂直平分线上一点.
的垂直平分线上一点.
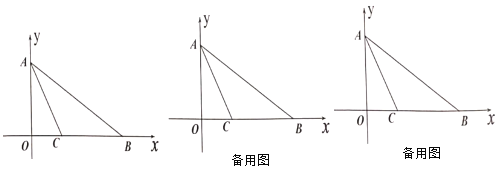
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以每秒2个单位长度的速度向终点
出发以每秒2个单位长度的速度向终点![]() 运动(点
运动(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 、
、![]() ,若点
,若点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,过点![]() 作
作![]() 垂直
垂直![]() 轴,交
轴,交![]() 于
于![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com