
【题目】分别以□ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.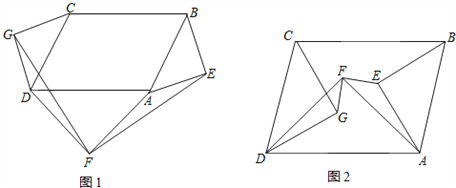
【答案】解:(1)GF⊥EF,GF=EF。
(2)GF⊥EF,GF=EF成立。理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,∠DAB+∠ADC=180°。
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°
∴∠BAE+∠FDA+∠EAF+∠ADF+∠FDC=180°。∴∠EAF+∠CDF=45°。
∵∠CDF+∠GDF=45°,∴∠FDG=∠EAF。
∵在△EAF和△GDF中, 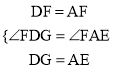 ,∴△EAF≌△GDF(SAS)。
,∴△EAF≌△GDF(SAS)。
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA。
∴∠GFE=90°。∴GF⊥EF。
【解析】试题分析:根据等腰直角三角形的性质和平行四边形的性质来证明△FDG和△FAE全等,从而得到FG=EF,∠DFG=∠AFE,根据∠DFA=90°得出∠GFE=90°,即EF⊥FG.
试题解析:(1)答:在图1中,GF=EF且GE⊥EF
(2)、∵四边形ABCD是平行四边形
∴AB=DC,且AB∥DC. 又∵△ABE、△CDG是等腰三角形
∴AE=BE=DG=CG,∠CDG=∠BAE=45°
又∵△AFD是等腰三角形,
∴AF=DF,∠FDA=∠DAF=45°,∠AFD=90°
又∵AB∥DC ∴∠CDA+∠DAB=180°
又∵∠CDA=90°-∠FDG;∠DAB=90°+∠FAE
∴90°-∠FDG+90°+∠FAE=180°
∴∠FDG=∠FAE
∴△FDG≌△FAE(SAS).
∴FG=FE,∠DFG=∠AFE
又∵∠DFG+∠GFA=90°,
∴∠AFE+∠GFA=90°.
∴EE⊥GF


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片上有一点P,PA=1,PD=2,PC=3,现将△PCD剪下,并将它拼到如图所示位置(C与A重合,P与G重合,D与D重合),则∠APD的度数为( )

A.150°B.135°C.120°D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车间同时开始加工一批服装,从开始加工到完成这批服装甲车间工作了8小时,乙车间在中途停工一段时间维修设备,然后在甲车间加工到4小时时按停工前的工作效率继续加工,直至与甲车间同时完成这批服装的加工任务.设甲、乙两车间各自加工服装的数量为![]() (件),甲车间加工的时间为
(件),甲车间加工的时间为![]() (时),
(时),![]() 与
与![]() 的函数图象如图所示.
的函数图象如图所示.
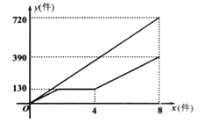
(1)甲车间每小时加工服装的件数为________件,这批服装的总件数为________件;
(2)乙车间花了多少时间维修设备?
(3)求甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
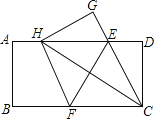
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
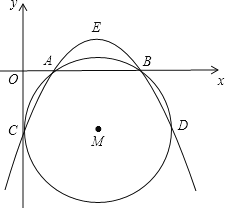
【题目】如图,在直角坐标系中,抛物线y=a(x-![]() )2+
)2+![]() 与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
(1)求a值及A,B两点坐标;
(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角时,请求出m的取值范围;
(3)点E是抛物线的顶点,⊙M沿CD所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程队,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元. 工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成;
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y= ![]() x+2与x轴,y轴分别相交于A、B两点,与反比例函数y=
x+2与x轴,y轴分别相交于A、B两点,与反比例函数y= ![]() (x>0)的图象相交于点C(2,3).点P是反比例函数图象上一点,作PE垂直x轴于E,若以P、O、E为顶点的三角形与△AOB相似,则点P的坐标是________.
(x>0)的图象相交于点C(2,3).点P是反比例函数图象上一点,作PE垂直x轴于E,若以P、O、E为顶点的三角形与△AOB相似,则点P的坐标是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com