
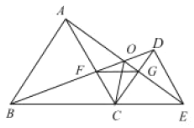
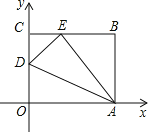
【题目】如图,已知![]() 和
和![]() 均是等边三角形,点
均是等边三角形,点![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ﹔④
﹔④![]() ,其中正确结论有_________个.
,其中正确结论有_________个.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 方向向点
方向向点![]() 运动,
运动,![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
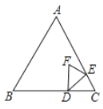
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 上;
上;
(2)当![]() 时,求
时,求![]() 与
与![]() 的数量关系;
的数量关系;
(3)当点![]() 、
、![]() 、
、![]() 三点共线时,求证:点
三点共线时,求证:点![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
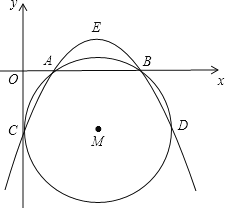
【题目】如图,在直角坐标系中,抛物线y=a(x-![]() )2+
)2+![]() 与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
(1)求a值及A,B两点坐标;
(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角时,请求出m的取值范围;
(3)点E是抛物线的顶点,⊙M沿CD所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
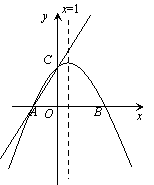
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
(1)求D、E两点的坐标.
(2)求过D、E两点的直线函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )

A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com