
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
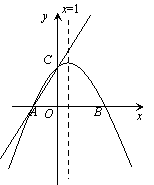
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
【答案】(1)![]() ,y=
,y=![]() x2+
x2+![]() x+
x+![]() ;(2)(1,3);(3)存在,5.2 ,7.2;(4)是.
;(2)(1,3);(3)存在,5.2 ,7.2;(4)是.
【解析】
试题(1)首先求得m的值和直线的解析式,根据抛物线对称性得到B点坐标,根据A、B点坐标利用交点式求得抛物线的解析式;
(2)确定何时△ACP的周长最小.利用轴对称的性质和两点之间线段最短的原理解决;确定P点坐标P(1,3),从而直线M1M2的解析式可以表示为y=kx+3-k;
(3)存在, 设Q(x,-![]() x2+
x2+![]() x+
x+![]() )①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
)①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
(4)利用两点间的距离公式,分别求得线段M1M2、M1P和M2P的长度,相互比较即可得到结论:![]() 为定值.
为定值.
试题解析:(1)∵y=![]() x+m经过点(-3,0),
x+m经过点(-3,0),
∴0=![]() +m,解得m=
+m,解得m=![]() ,
,
∴直线解析式为y=![]() x+
x+![]() ,C(0,
,C(0,![]() ).
).
∵抛物线y=ax2+bx+c对称轴为x=1,且与x轴交于A(-3,0),∴另一交点为B(5,0),
设抛物线解析式为y=a(x+3)(x-5),
∵抛物线经过C(0,![]() ),
),
∴![]() =a3(-5),解得a=
=a3(-5),解得a=![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+
x+![]() ;
;
(2)要使△ACP的周长最小,只需AP+CP最小即可.如图2,
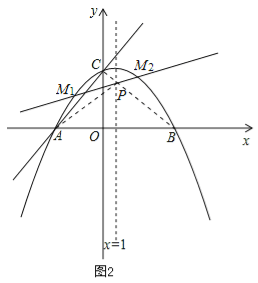
连接BC交x=1于P点,因为点A、B关于x=1对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小(AP+CP最小值为线段BC的长度).
∵B(5,0),C(0,![]() ),
),
∴直线BC解析式为y=![]() x+
x+![]() ,
,
∵xP=1,∴yP=3,即P(1,3).
(3) (3)存在 设Q(x, ![]() x2+
x2+![]() x+
x+![]() )
)
①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2
②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2
∴Q的横坐标为5.2 ,7.2
(4)令经过点P(1,3)的直线为y=kx+b,则k+b=3,即b=3-k,
则直线的解析式是:y=kx+3-k,
∵y=kx+3-k,y=![]() x2+
x2+![]() x+
x+![]() ,
,
联立化简得:x2+(4k-2)x-4k-3=0,
∴x1+x2=2-4k,x1x2=-4k-3.
∵y1=kx1+3-k,y2=kx2+3-k,∴y1-y2=k(x1-x2).
根据两点间距离公式得到:![]()
![]()
∴![]() =4(1+k2).
=4(1+k2).
又![]()
![]() ;
;
同理![]()
∴![]()
![]()
![]()
=4(1+k2).
∴M1PM2P=M1M2,
∴![]() 为定值.
为定值.
考点: 二次函数综合题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
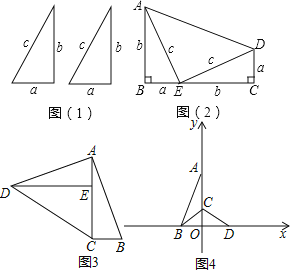
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形构造图3的图形,你能利用这个图形证明出题(1)的结论吗?如果能,请写出证明过程;
(3)当a=3,b=4时,将其中一个直角三角形放入平面直角坐标系中,使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合(如图4中Rt△AOB的位置).点C为线段OA上一点,将△ABC沿着直线BC翻折,点A恰好落在x轴上的D处.
①请写出C、D两点的坐标;
②若△CMD为等腰三角形,点M在x轴上,请直接写出符合条件的所有点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )

A. 当BC等于0.5时,l与⊙O相离
B. 当BC等于2时,l与⊙O相切
C. 当BC等于1时,l与⊙O相交
D. 当BC不为1时,l与⊙O不相切
查看答案和解析>>
科目:初中数学 来源: 题型:
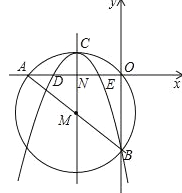
【题目】如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(﹣8,0),B(0,﹣6)两点.
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
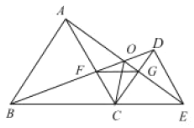
【题目】如图,已知![]() 和
和![]() 均是等边三角形,点
均是等边三角形,点![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ﹔④
﹔④![]() ,其中正确结论有_________个.
,其中正确结论有_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).

解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
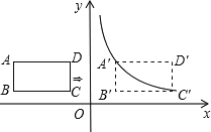
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,![]() ),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=
),AB=1,AD=2,将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y=![]() 的图象上,得矩形A′B′C′D′,则反比例函数的解析式为______.
的图象上,得矩形A′B′C′D′,则反比例函数的解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2;④当x>0时,y随x的增大而减小.正确结论的个数是( )
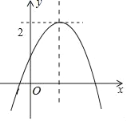
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
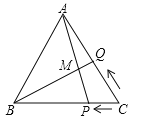
【题目】如图,等边![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,点
匀速运动,点![]() 从点
从点![]() 出发,以
出发,以![]() 秒的速度由
秒的速度由![]() 向
向![]() 匀速运动,
匀速运动,![]() 、
、![]() 交于点
交于点![]() ,当点
,当点![]() 到达
到达![]() 点时,
点时,![]() 、
、![]() 两点停止运动,设
两点停止运动,设![]() 、
、![]() 两点运动的时间为
两点运动的时间为![]() 秒,若
秒,若![]() 时,则
时,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com