
【题目】如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )

A. 当BC等于0.5时,l与⊙O相离
B. 当BC等于2时,l与⊙O相切
C. 当BC等于1时,l与⊙O相交
D. 当BC不为1时,l与⊙O不相切
【答案】D
【解析】
试题根据圆心到直线的距离大于半径,直线与圆相离,圆心到直线的距离小于半径,直线与圆相交;圆心到直线的距离等于半径,直线与圆相切,可得
A、∵BC=0.5,∴OC=OB+CB=1.5;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=0.5<1,∴l与⊙O相交,故A错误;
OC=0.5<1,∴l与⊙O相交,故A错误;
B、∵BC=2,∴OC=OB+CB=3;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=1.5>1,∴l与⊙O相离,故B错误;
OC=1.5>1,∴l与⊙O相离,故B错误;
C、∵BC=1,∴OC=OB+CB=2;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=1,∴l与⊙O相切,故C错误;
OC=1,∴l与⊙O相切,故C错误;
D、∵BC≠1,∴OC=OB+CB≠2;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC≠1,∴l与⊙O不相切,故D正确;
OC≠1,∴l与⊙O不相切,故D正确;
故选:D.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
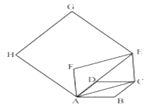
【题目】如图,边长为1的菱形![]() 中,
中,![]() ,连结对角线
,连结对角线![]() ,以
,以![]() 为边做第二个菱形
为边做第二个菱形![]() ,
,![]() .连结
.连结![]() ,再以
,再以![]() 为边做第三个菱形
为边做第三个菱形![]() ,使
,使![]() …按此规律所作的第2015个菱形的边长是__________.
…按此规律所作的第2015个菱形的边长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
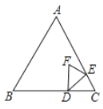
【题目】如图,等边![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 方向向点
方向向点![]() 运动,
运动,![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 上;
上;
(2)当![]() 时,求
时,求![]() 与
与![]() 的数量关系;
的数量关系;
(3)当点![]() 、
、![]() 、
、![]() 三点共线时,求证:点
三点共线时,求证:点![]() 为线段
为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
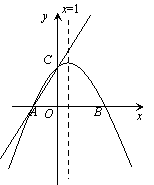
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
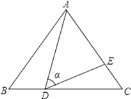
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com