
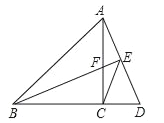
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
【答案】(1)证明见解析;(2)45°;(3)BE=AE+![]() CE.
CE.
【解析】
试题(1)由垂直的定义得到∠ACB=90°根据全等三角形的判定定理即可得到结论;
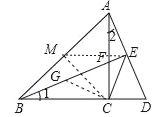
(2)取AB的中点M,连接CM,EM,根据圆周角定理即可得到结论;
(3)作CG⊥CE交BE于G,根据等腰直角三角形的性质得到CG=CE,根据全等三角形的性质得到BG=AE,于是得到结论.
试题解析:解:(1)∵BE⊥AD,∠ACB=90°,∴∠1=∠2=90°﹣∠D,在△BCF和△ACD中,∵∠1=∠2,BC=AC,∠BCF=∠ACD=90°,∴△BCF≌△ACD;
(2)∠BEC=45°.理由:取AB的中点M,连接CM,EM,则CM=EM=![]() AB=AM=BM,∴点A,B,C,E在同一个圆(⊙M)上,∴∠BEC=∠BAC=45°;
AB=AM=BM,∴点A,B,C,E在同一个圆(⊙M)上,∴∠BEC=∠BAC=45°;
(3)BE=AE+![]() CE.证明如下:
CE.证明如下:
作CG⊥CE交BE于G,∵∠BEC=45°,则∠CGE=45°=∠BEC,CG=CE,∴∠BGC=135°=∠AEC,EG=![]() CE,在△BCG和△ACE中,∵∠1=∠2,∠BGC=∠AEC,BC=AC,∴△BCG≌△ACE,∴BG=AE,∴BE=BG+EG=AE+
CE,在△BCG和△ACE中,∵∠1=∠2,∠BGC=∠AEC,BC=AC,∴△BCG≌△ACE,∴BG=AE,∴BE=BG+EG=AE+![]() CE.
CE.


科目:初中数学 来源: 题型:
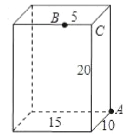
【题目】如图,长方形的长为15,宽为10,高为20,点![]() 离点
离点![]() 的距离为5,蚂蚁如果要沿着长方形的表面从点
的距离为5,蚂蚁如果要沿着长方形的表面从点![]() 爬到点
爬到点![]() ,需要爬行的最短距离是( )
,需要爬行的最短距离是( )
A.35B.![]() C.25D.
C.25D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子在![]() 轴上及第一象限内运动,第1次从
轴上及第一象限内运动,第1次从![]() 运动到
运动到![]() ,第2次从
,第2次从![]() 运动到
运动到![]() ,第3次从
,第3次从![]() 运动到
运动到![]() ,它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )
,它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一边长为4正方形![]() 放在平面直角坐标系中,其中
放在平面直角坐标系中,其中![]() 为原点,点
为原点,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,
轴上,![]() 为射线
为射线![]() 上任意一点
上任意一点
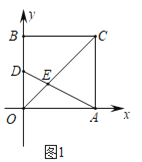
(1)如图1,若点![]() 坐标为
坐标为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的面积为__________;
的面积为__________;
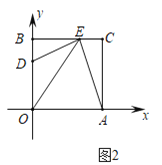
(2)如图2,将![]() 沿
沿![]() 翻折得
翻折得![]() ,若点
,若点![]() 在直线
在直线![]() 图象上,求出
图象上,求出![]() 点坐标;
点坐标;
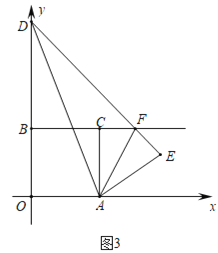
(3)如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() 和射线
和射线![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,平面内是否存在点
,平面内是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的等腰直角三角形,若存在,请求出所有点
为直角边的等腰直角三角形,若存在,请求出所有点![]() 坐标:若不存在,请说明理由.
坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
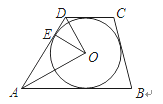
【题目】如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(1)求证:AO2=AEAD;
(2)若AO=4cm,AD=5cm,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
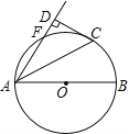
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且点C为弧BF的中点,连接AC、AF,过点C作CD⊥AF交AF延长线于点D.
(1)求证:CD是⊙O的切线;
(2)判断线段AB、AF与AD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某校对各个班级的教室卫生检查成绩如下表所示:
地面 | 门窗 | 桌椅 | 黑板 | |
一班 |
|
|
|
|
二班 |
|
|
|
|
三班 |
|
|
|
|
(1)若按平均成绩计算,哪班卫生成绩最好?
(2)若将地面、门窗、桌椅、黑板按![]() ,
,![]() ,
,![]() ,
,![]() 的比例计算各班卫生成绩,那么哪个班的成绩最高?
的比例计算各班卫生成绩,那么哪个班的成绩最高?
(3)试统计你校八年级各个班地面、门窗、桌椅、黑板的卫生成绩,并分别按(1)、(2)的评分标准计算成绩,看看你所在班级的卫生情况,你将怎样继续改进?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com